【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种球共20个,某学习小组做摸球实验,每次摸出一个球再把它放回袋中,不断重复,下表是一次摸球实验的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近多少?
(2)试估算口袋里黑、白两种颜色的球各有多少个?
参考答案:
【答案】(1)0.6(2)12;8
【解析】(1)观察表格可知,当摸球次数越来越大,摸到白球的频率在0.6左右摆动,据此即可解答;(2)用球的总数乘以摸到白球的概率即可确定白球的个数,从而求出黑球的个数.
(1)当n≥500,频率值稳定在0.6左右,由此,当n很大时,摸到白球的频率将会接近0.6.
(2)白球个数:20×0.6=12(个),黑球个数:20-12=8(个).
-
科目: 来源: 题型:
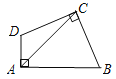
查看答案和解析>>【题目】如图,在四边形ABCD中,∠DAB=∠DCB=90°,CB=CD,AC=6,则四边形ABCD的面积是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x,y,并以此确定点P(x,y),那么点P落在直线y=-2x+9上的概率为( )
A.
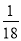 B.
B. 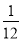 C.
C. 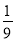 D.
D. 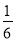
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a,b,将其作为M点的横、纵坐标,则点M(a,b)落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图),然后将剩余部分拼成一个长方形(如图).

(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2-2ab+b2=(a-b)2 B.a2-b2=(a+b)(a-b) C.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值.
②计算:(1-
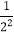 )(1-
)(1- )(1-
)(1-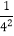 )…(1-
)…(1-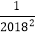 )(1-
)(1- ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
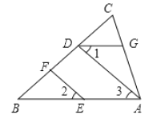
解:因为EF∥AD
所以∠2= ( )
又因为∠1=∠2
所以∠1=∠3( )
所以AB∥ ( )
所以∠BAC+ =180°( )
因为∠BAC=70°
所以∠AGD= .
相关试题

