【题目】如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a,b,将其作为M点的横、纵坐标,则点M(a,b)落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】C.
【解析】
试题分析:解:列举出事件:(-2,1),(-2,0),(-2,2),(0,-2),(0,1),(0,2),(1,2),(1,0),(1,-2),(2,-2),(2,0),(2,1)共有12种结果,
而落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)有:(-2,0),(0,1),(0,2),(1,0),(2,0),(-1,0)共6中可能情况,
所以落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是=![]() ,
,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不解方程,求下列各方程的两根之和与两根之积:
(1)x2+2x+1=0; (2)3x2-2x-1=0; (3)2x2+3=7x2+x; (4)5x-5=6x2-4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分成12cm和15cm两部分,求△ABC各边的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程mx2-2mx+m-2=0.
(1)若方程有两实数根,求m的范围.
(2)设方程两实根为x1,x2,且|x1-x2|=1,求m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB.
(1)求证:∠OAC=∠OCA;
(2)如图②,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P,即满足∠POC=
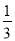 ∠AOC,∠PCE=
∠AOC,∠PCE=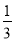 ∠ACE,求∠P的大小;
∠ACE,求∠P的大小;(3)如图③,在(2)中,若射线OP、CP满足∠POC=
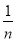 ∠AOC,∠PCE=
∠AOC,∠PCE= ∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示).
∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示).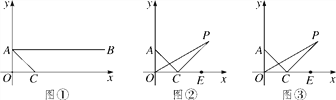
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于
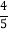 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,线段
 和射线
和射线 交于点
交于点 .
.(
 )利用尺规完成以下作图,并保留作图痕迹(不写作法).
)利用尺规完成以下作图,并保留作图痕迹(不写作法).①在射线
 上作一点
上作一点 ,使
,使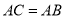 ,连接
,连接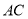 ;
;②作
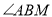 的角平分线交
的角平分线交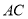 于
于 点;
点;③在射线
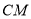 上作一点
上作一点 ,使
,使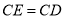 ,连接
,连接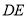 .
.(
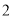 )在(
)在(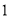 )所作的图形中,通过观察和测量可以发现
)所作的图形中,通过观察和测量可以发现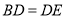 ,请将下面的证明过程补充完整.
,请将下面的证明过程补充完整.
证明:∵
 ,
,∴
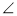 __________
__________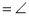 __________,①
__________,①∵
 平分
平分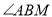 ,
,∴
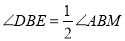 ,
,∴
 __________,②
__________,②∵
 ,
,∴
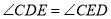 ,
,∵
 ,
,∴
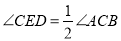 ,
,∴
 ,
,∴
 .( )
.( )
相关试题

