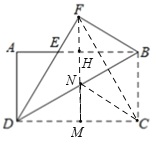
【题目】如图,把一张长方形纸片ABCD沿对角线BD对折,使得点C落在点F处,DF交AB于E,AD=8,AB=16.
(1)求证:DE=BE;
(2)求S△BEF;
(3)若M、N分别为线段CD、DB上的动点,直接写出(NC+NM)的最小值___________.

参考答案:
【答案】(1)证明见解析;(2)S△BDE=40;(3)12.8.
【解析】
(1)由折叠的性质可得到∠BDC=∠BDF,再由平行线的性质可得∠ABD=∠BDC,由此可得∠ABD=∠BDF,据此即可得结论;
(2)设BE=x,则DE=BE=x,AE=16-x,利用勾股定理即可求出BE的长,再利用三角形面积公式进行求解即可得答案;
(3)由题意知C、F关于直线BD对称,过点F作FM⊥CD,垂足为M,交BD于点N,交AB于点H,此时MN+NC的值最小,求出FH的长即可求得答案.
(1)∵△BCD≌△BFD,
∴∠BDC=∠BDF,
又∵四边形ABCD是长方形,
∴AB∥DC,
∴∠ABD=∠BDC,
∴∠ABD=∠BDF,
∴DE=BE;
(2)∵四边形ABCD是矩形,
∴∠A=90°,
∴AD2+AE2=DE2,
设BE=x,则DE=BE=x,AE=AB-BE=16-x,
∴82+(16-x)2=x2,
∴x=10,
∴S△BDE=![]() =40;
=40;
(3)由题意知C、F关于直线BD对称,过点F作FM⊥CD,垂足为M,交BD于点N,交AB于点H,此时MN+NC的值最小,
∵四边形ABCD是矩形,
∴AB//CD,∠A=∠ADM=90°,
∵FM⊥CD,
∴∠FMD=90°,
∴四边形ADMH是矩形,
∴∠FHE=90°,HM=AD=8,
∵∠A=∠BFE=90°,AD=BF,DE=BE,
∴Rt△ADE≌Rt△FBE(HL),
∴EF=AE=16-10=6,
∵S△BEF=![]() ,
,
∴FH=![]() =4.8,
=4.8,
∴FM=FH+HM=4.8+8=12.8,
即NC+NM的最小值为12.8,
故答案为:12.8.
-
科目: 来源: 题型:
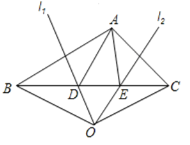
查看答案和解析>>【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连结OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
-
科目: 来源: 题型:
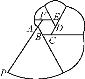
查看答案和解析>>【题目】如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( )
A. 13π cm B. 14π cm C. 15π cm D. 16π cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是考古学家发现的古代钱币的一部分,合肥一中的小明正好学习了圆的知识,他想求其外圆半径,连接外圆上的两点A,B,并使AB与内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10 cm,AB=60 cm,则这个钱币的外圆半径为__cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:

如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是___________;
(2)问题解决: 如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,以C为顶点作∠ECF,使得角的两边分别交AB,AD于E、F两点,连接EF,且EF=BE+DF,试探索∠ECF与∠A之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BE、CF分别是钝角△ABC(∠A>90°)的高,在BE上截取BP=AC,在CF的延长线截取CQ=AB,连结AP、AQ,请推测AP与AQ的数量和位置关系并加以证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
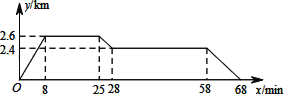
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间.
相关试题

