【题目】如图,BE、CF分别是钝角△ABC(∠A>90°)的高,在BE上截取BP=AC,在CF的延长线截取CQ=AB,连结AP、AQ,请推测AP与AQ的数量和位置关系并加以证明。

参考答案:
【答案】AP=AQ,AP⊥AQ,理由见解析
【解析】
先证明△APB≌△QAC,得AP=AQ,∠BAP=∠CQA,通过等量代换得∠BAP+∠QAF=90°即可得AP⊥AQ.
解:AP=AQ,AP⊥AQ,理由如下:
∵CF⊥AB,BE⊥AC,
∴∠AEB=∠AFC=90°,
∴∠ABE=∠ACQ=∠BAC﹣90°.
∵BP=AC,CQ=AB,
在△APB和△QAC中,
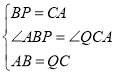 ,
,
∴△APB≌△QAC(SAS).
∴∠BAP=∠CQA,AP=AQ,
∵∠CQA+∠QAF=90°,
∴∠BAP+∠QAF=90°.
即AP⊥AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是考古学家发现的古代钱币的一部分,合肥一中的小明正好学习了圆的知识,他想求其外圆半径,连接外圆上的两点A,B,并使AB与内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10 cm,AB=60 cm,则这个钱币的外圆半径为__cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD沿对角线BD对折,使得点C落在点F处,DF交AB于E,AD=8,AB=16.
(1)求证:DE=BE;
(2)求S△BEF;
(3)若M、N分别为线段CD、DB上的动点,直接写出(NC+NM)的最小值___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:

如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是___________;
(2)问题解决: 如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,以C为顶点作∠ECF,使得角的两边分别交AB,AD于E、F两点,连接EF,且EF=BE+DF,试探索∠ECF与∠A之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
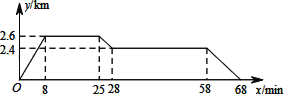
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:根据《中国铁路中长期发展规划》,预计到2020年底,我国建设城际轨道交通的公里数是客运专线的2倍。其中建设城际轨道交通约投入8000亿元,客运专线约投入3500亿元。据了解,建设每公里城际轨道交通与客运专线共需1.5亿元。预计到2020年底,我国将建设城际轨道交通和客运专线分别约多少公里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
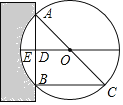
A. 13寸 B. 20寸 C. 26寸 D. 28寸
相关试题

