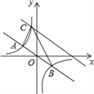
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
参考答案:
【答案】(1) y=﹣![]() ;(2) y=﹣
;(2) y=﹣![]() x+8.
x+8.
【解析】试题分析:(1)根据题意,将y=3代入一次函数的解析式,求出x的值,得到A点的坐标,再利用反比例函数的坐标特征求出反比例函数的解析式;
(2)根据A、B点关于原点对称,可求出B点的坐标及线段AB的长度,设出平移后的直线解析式,根据平行线间的距离,由三角形的面积求出关于b的一元一次方程即可求解.
试题解析:(1)令一次函数y=﹣![]() x中y=3,则3=﹣
x中y=3,则3=﹣![]() x,
x,
解得:x=﹣6,即点A的坐标为(﹣6,3).
∵点A(﹣6,3)在反比例函数y=![]() 的图象上,
的图象上,
∴k=﹣6×3=﹣18,
∴反比例函数的表达式为y=﹣![]() .
.
(2)设平移后直线于y轴交于点F,连接AF、BF如图所示.
设平移后的解析式为y=﹣![]() x+b,
x+b,
∵该直线平行直线AB,
∴S△ABC=S△ABF,
∵△ABC的面积为48,
∴S△ABF=![]() OF(xB﹣xA)=48,
OF(xB﹣xA)=48,
由对称性可知:xB=﹣xA,
∵xA=﹣6,
∴xB=6,
∴![]() b×12=48,
b×12=48,
∴b=8.
∴平移后的直线的表达式为:y=﹣![]() x+8.
x+8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1、x2是一元二次方程x2﹣3x+2=0的两个实根,则x1+x2等于( )
A.﹣3
B.3
C.﹣2
D.2 -
科目: 来源: 题型:
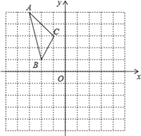
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )
A. 3:5B. 9:25C. 5:3D. 25:9
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2(x+1)2﹣2的图象先向左平移1个单位长度,再向上平移3个单位长度,则顶点坐标为( )
A.(﹣2,1)
B.(2,1)
C.(0,1)
D.(﹣2,﹣5) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是摩天轮的圆心,长为110米的AB是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A的仰角为33°,测得圆心O的仰角为21°,则小莹所在C点到直径AB所在直线的距离约为(tan33°≈0.65,tan21°≈0.38)( )

A. 169米 B. 204米 C. 240米 D. 407米
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:﹣x2﹣4y2+4xy=_____.
相关试题

