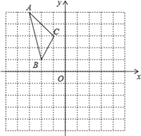
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
参考答案:
【答案】(1)点A1的坐标为(2,2),B1点的坐标为(3,﹣2);(2)A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);(3)△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);
【解析】试题分析:(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
试题解析:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的度数比它的余角的度数大20°,则这个角的度数是( ).
A. 20° B. 55° C. 45° D. 35°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.

(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1、x2是一元二次方程x2﹣3x+2=0的两个实根,则x1+x2等于( )
A.﹣3
B.3
C.﹣2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )
A. 3:5B. 9:25C. 5:3D. 25:9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=﹣
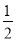 x与反比例函数y=
x与反比例函数y=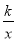 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.(1)求反比例函数的表达式;
(2)将直线y=﹣
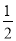 x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.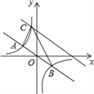
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2(x+1)2﹣2的图象先向左平移1个单位长度,再向上平移3个单位长度,则顶点坐标为( )
A.(﹣2,1)
B.(2,1)
C.(0,1)
D.(﹣2,﹣5)
相关试题

