【题目】如图所示,在平面内,给定不在同一直线上的点![]() ,
,![]() ,
,![]() ,射线
,射线![]() 是
是![]() 的平分线,点
的平分线,点![]() 到点
到点![]() ,
,![]() ,
,![]() 的距离均等于
的距离均等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() ,图形
,图形![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,作
,作![]() 于点
于点![]() ,延长
,延长![]() 交图形
交图形![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,求直线
,求直线![]() 与图形
与图形![]() 的公共点个数.
的公共点个数.
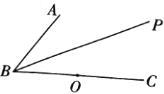
参考答案:
【答案】(1)证明见解析;(2)1个.
【解析】
(1)利用圆的定义得到图形G为△ABC的外接圆⊙O,由∠ABD=∠CBD可得到弧AD等于弧CD,从而圆周角、弧、弦的关系得到AD=CD;
(2)如图,证明CD=CM,则可得到BC垂直平分DM,利用垂径定理得到BC为直径,再证明OD⊥DE,从而可判断DE为⊙O的切线,于是得到直线DE与图形G的公共点个数.
(1)证明:∵到点O的距离等于a的所有点组成图形G,
∴图形G为△ABC的外接圆⊙O,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴![]() ,
,
∴AD=CD;
(2)如图,
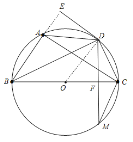
∵AD=CM,AD=CD,
∴CD=CM,
∵DM⊥BC,
∴BC垂直平分DM,
∴BC为直径,
∴∠BAC=90°,
∵![]() ,
,
∴OD⊥AC,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥DE,
∴DE为⊙O的切线,
∴直线DE与图形G的公共点个数为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进
 、
、 两种粽子1100个,购买
两种粽子1100个,购买 种粽子与购买
种粽子与购买 种粽子的费用相同,已知
种粽子的费用相同,已知 粽子的单价是
粽子的单价是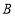 种粽子单价的1.2倍.
种粽子单价的1.2倍.(1)求
 、
、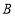 两种粽子的单价各是多少?
两种粽子的单价各是多少?(2)若计划用不超过7000元的资金再次购买
 、
、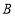 两种粽子共2600个,已知
两种粽子共2600个,已知 、
、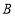 两种粽子的进价不变,求
两种粽子的进价不变,求 中粽子最多能购进多少个?
中粽子最多能购进多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有若干间标准房,当标准房的价格为
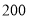 元时,每天入住的国间数为
元时,每天入住的国间数为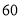 间,经市场调查表明,该宾馆每间标准房的价格在
间,经市场调查表明,该宾馆每间标准房的价格在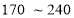 元之间(含
元之间(含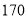 元,
元,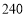 元)浮动时,每天人住的房间数
元)浮动时,每天人住的房间数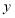 (间)与每间标准房的价格
(间)与每间标准房的价格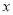 (元)的数据如下表:
(元)的数据如下表: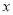 (元)
(元)……
190
200
210
220
……
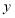 (元)
(元)……
65
60
55
50
……
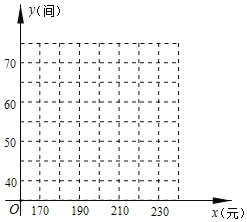
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)猜想(1)中的图象是什么函数的图象,求
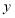 关于
关于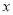 的函数表达式,并写出自变量
的函数表达式,并写出自变量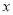 的取值范围.
的取值范围.(3)设客房的日营业额为W (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
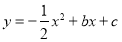 过点
过点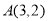 ,且与直线
,且与直线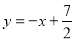 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为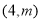 .
.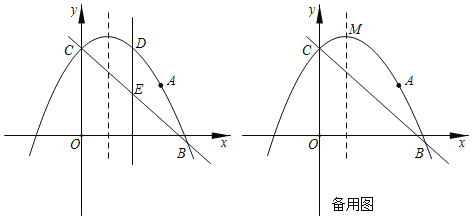
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线
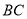 上方的一点,过点D作
上方的一点,过点D作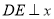 轴交直线
轴交直线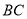 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段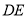 的长度最大时,求
的长度最大时,求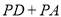 的最小值;
的最小值;(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使
 ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年是我国建国70周年,回顾过去展望未来,创新是引领发展的第一动力,北京科技创新能力不断增强,下面的统计图反映了2010﹣2018年北京市每万人发明专利申请数与授权数的情况.
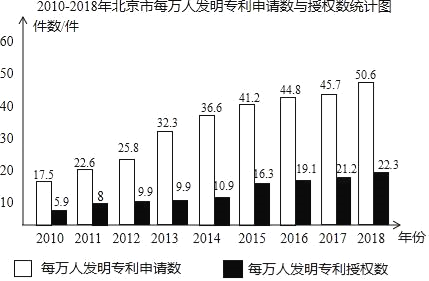
根据统计图提供的信息,下列推断合理的是( )
A. 2010﹣2018年,北京市毎万人发明专利授权数逐年增长
B. 2010﹣2018年,北京市毎万人发明专利授权数的平均数超过10件
C. 2010年申请后得到授权的比例最低
D. 2018年申请后得到授权的比例最高
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下表所示:
弹簧总长L(cm)
16
17
18
19
20
重物重量x(kg)
0.5
1.0
1.5
2.0
2.5
当重物质量为5kg(在弹性限度内)时,弹簧总长L(cm)是( )
A.22.5B.25C.27.5D.30
相关试题

