【题目】在四边形ABCD中,AB=3,BC=4,AD=5 ![]() ,CD=5,∠ABC=90°,求对角线BD的长.
,CD=5,∠ABC=90°,求对角线BD的长. 
参考答案:
【答案】解:作DM⊥BC,交BC延长线于M,连接AC,如图所示: 
则∠M=90°,
∴∠DCM+∠CDM=90°,
∵∠ABC=90°,AB=3,BC=4,
∴AC2=AB2+BC2=25,
∴AC=5,
∵AD=5 ![]() ,CD=5,
,CD=5,
∴AC2+CD2=AD2 ,
∴△ACD是直角三角形,∠ACD=90°,
∴∠ACB+∠DCM=90°,
∴∠ACB=∠CDM,
∵∠ABC=∠M=90°,
∴△ABC∽△CMD,
∴ ![]() =
= ![]() =
= ![]() =1,
=1,
∴CM=AB=5,DM=BC=4,
∴BM=BC+CM=9,
∴BD= ![]() =
= ![]() =
= ![]() .
.
【解析】作DM⊥BC,交BC延长线于M,连接AC,由勾股定理得出AC2=AB2+BC2=25,求出AC2+CD2=AD2 , 由勾股定理的逆定理得出△ACD是直角三角形,∠ACD=90°,证出∠ACB=∠CDM,得出△ABC∽△CMD,由相似三角形的对应边成比例求出CM=AB=5,DM=BC=4,得出BM=BC+CM=9,再由勾股定理求出BD即可.
【考点精析】通过灵活运用勾股定理的概念和勾股定理的逆定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=2(x﹣1)(x+5)的图象与x轴的两个交点之间的距离是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A的坐标是(2,8),则点A在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,ACB的顶点A在△ECD的斜边DE上
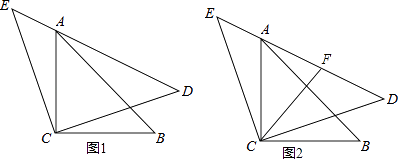
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=2,AC=2 ,点F是AD的中点,直接写出CF的长是 .
,点F是AD的中点,直接写出CF的长是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.
(2)用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正比例函数的图象与一个反比例函数的一个交点坐标为(1,3),则另一个交点坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(﹣2,﹣2)都是“平衡点”.当﹣1≤x≤3时,直线y=2x+m上有“平衡点”,则m的取值范围是( )
A.0≤m≤1
B.﹣3≤m≤1
C.﹣3≤m≤3
D.﹣1≤m≤0
相关试题

