【题目】如图,在△ABC中,D为AC边上一点,∠DBC=∠A.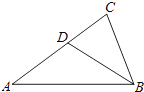
(1)求证:△BCD∽△ACB;
(2)如果BC= ![]() ,AC=3,求CD的长.
,AC=3,求CD的长.
参考答案:
【答案】
(1)
证明:∵∠DBC=∠A,∠C=∠C,
∴△BCD∽△ACB;
(2)
解:∵△BCD∽△ACB,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CD=2.
【解析】(1)根据相似三角形的判定得出即可;(2)根据相似得出比例式,代入求出即可.
【考点精析】利用相似三角形的性质和相似三角形的判定对题目进行判断即可得到答案,需要熟知对应角相等,对应边成比例的两个三角形叫做相似三角形;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进冰箱、彩电进行销售,已知冰箱的进货单价比彩电的进货单价多400元,若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等.该商场冰箱、彩电的售货单价如下表:
冰箱
彩电
售价(元/台)
2500
2000
(1)分别求出冰箱、彩电的进货单价.
(2)为了满足市场需求,商场决定用不超过90 000元的资金采购冰箱、彩电共50台。若该商场将购进的冰箱、彩电共50台全部售出,获得利润为w元,为了使商场的利润最大,该商场该如何购进冰箱、彩电,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,点D在线段BC的延长线上移动,若∠BAC=40
 ,求∠DCE的度数.
,求∠DCE的度数.(2)设∠BAC=m,∠DCE=n.
①如图,当点D在线段BC的延长线上移动时,m与n之间有什么数量关系?请说明理由.
②当点D在直线BC上(不与B、C重合)移动时,m与n之间有什么数量关系?请直接写出你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,② AQ=BQ,③BP=2PQ, ④AE+BD=AB,其正确的个数有( )个.
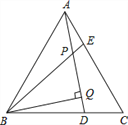
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点E,则△DEF的面积为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别.
(1)随机从箱子里取出1个球,则取出黄球的概率是多少?
(2)随机从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示出所有可能出现的结果,并求两次取出的都是白色球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数.

相关试题

