【题目】为了迎接2022年北京冬奥会,萍乡外国语学校组织了一次大型长跑比赛。甲,乙两人在比赛时,路程![]() (米)与时间
(米)与时间![]() (分钟)的关系如图所示,极据图像解答下列问题:
(分钟)的关系如图所示,极据图像解答下列问题:

(1)这次长跑比赛的全程是___米;先到达终点的人比另一个人领先____分钟:
(2)乙是学校田径队运动员,十分注意比赛技巧,比赛过程分起跑、途中跑冲刺跑三阶段,经历了两次加速过程.问第![]() 分钟时乙还落后甲多少米?
分钟时乙还落后甲多少米?
(3)假设乙在第一次加速后,始终保持这个速度继续前进。那么甲,乙两人谁先到达终点?请说明理由.
(4)事实上乙追上甲的时间是多少分钟?
参考答案:
【答案】(1)![]() ,
,![]() ;(2)乙落后甲
;(2)乙落后甲![]() ;(3)同时到达终点;(4)在第
;(3)同时到达终点;(4)在第![]() 分钟时乙追上甲.
分钟时乙追上甲.
【解析】
(1)根据图像即可求解;
(2)由图可知第四分钟时,乙走了1300米,只要求出甲的路程即可,根据甲到达终点时的数据可求出甲的速度,即可求出第四分钟的路程;
(3)由题意可求出2到4分钟时,乙走了(1300-600)米,因此可求出此时的速度,又可得剩下的路程为(2000-1300)米,故剩下的时间即可求出,然后求出甲剩下的时间进行比较,即可求解;
(4)甲追上乙时路程相同,冲刺时乙的路程为(2000-1300)米,时间为(5.4-4)分钟,那么可求出乙冲刺的速度,然后根据(2)求出的乙落后的距离,再求出追及的时间再加上前面的时间即可求出乙在第几分钟追上.
(1)这次长跑比赛的全程是2000米;先到达终点的人比另一个人领先6-5.4=0.6分钟:
(2)甲速度为![]() =
=![]() ,第四分钟时甲行驶了
,第四分钟时甲行驶了![]() 米,
米,
∴乙落后甲![]() -1300=
-1300=![]() 米.
米.
(3)途中乙的速度为(1300-600)÷(4-2)=![]() 米/分钟
米/分钟
剩下的路程还需时间(2000-1300)÷350=2分钟
所以乙在第一次加速后,始终保持这个速度继续前进甲,乙两人同时到达终点;
(4)冲刺时乙速度为(2000-1300)÷(5.4-4)=![]() 米/分钟
米/分钟
由(2)可知冲刺前还落后甲![]() 米.
米.
则追上甲还需![]() ÷(500-
÷(500-![]() )=0.2分钟
)=0.2分钟
4+0.2=4.2
故在第![]() 分钟时乙追上甲.
分钟时乙追上甲.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年大豆和小麦的总产量为200吨,今年大豆和小麦的总产量为225吨,其中大豆比去年増产5%,小麦比去年増产15%,求该农场今年大豆和小麦的产量各是多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( )

①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A. ③②④①B. ③④②①C. ①④②③D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料阅读:如图①所示的图形,像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
解决问题:
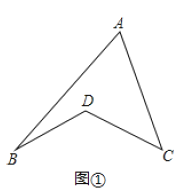
(1)观察“规形图”,试探究
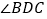 与
与 ,
, ,
,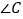 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下两个问题:
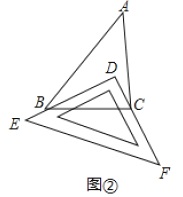
Ⅰ.如图②,把一块三角尺
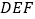 放置在
放置在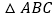 上,使三角尺的两条直角边
上,使三角尺的两条直角边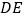 ,
,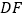 恰好经过点
恰好经过点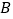 ,
,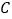 ,若
,若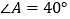 ,则
,则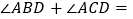 _____
_____ .
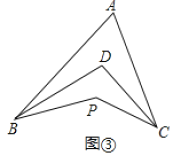
.Ⅱ.如图③,
 平分
平分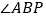 ,
,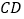 平分
平分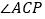 ,若
,若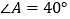 ,
,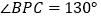 ,求
,求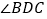 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
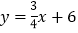 的图象与
的图象与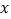 ,
,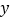 轴分别交于
轴分别交于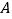 ,
,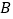 两点,点
两点,点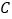 与点
与点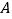 关于
关于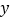 轴对称.动点
轴对称.动点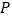 ,
,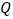 分别在线段
分别在线段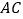 ,
,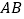 上(点
上(点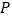 与点
与点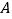 ,
,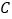 不重合),且满足
不重合),且满足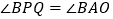 .
.(1)求点
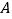 ,
,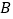 的坐标及线段
的坐标及线段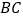 的长度;
的长度;(2)当点
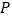 在什么位置时,
在什么位置时,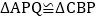 ,说明理由;
,说明理由;(3)当
 为等腰三角形时,求点
为等腰三角形时,求点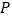 的坐标.
的坐标.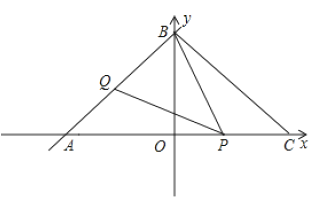
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A.
 B.
B.  C. 3 D.
C. 3 D. 
相关试题

