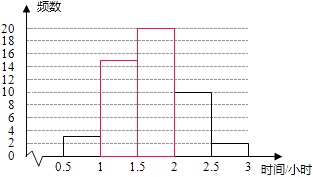
【题目】九年级(1)班开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,老师调查了全班50名学生在这次活动中做家务的时间,并将统计的时间(单位:小时)分成5组: A.0.5≤x<1 B.1≤x<1.5 C.1.5≤x<2 D.2≤x<2.5 E.2.5≤x<3;并制成两幅不完整的统计图(如图):
请根据图中提供的信息,解答下列问题:
(1)这次活动中学生做家务时间的中位数所在的组是;
(2)补全频数分布直方图;
(3)该班的小明同学这一周做家务2小时,他认为自己做家务的时间比班里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计知识说明理由.
参考答案:
【答案】
(1)C
(2)解:
(3)解:符合实际.
设中位数为m,根据题意,m的取值范围是1.5≤m<2,
∵小明帮父母做家务的时间大于中位数,
∴他帮父母做家务的时间比班级中一半以上的同学多.
【解析】解:(1)C组的人数是:50×40%=20(人), B组的人数是:50﹣3﹣20﹣10﹣2=15(人),
把这组数据按从小到大排列为,由于共有50个数,第25、26位都落在1.5≤x<2范围内,则中位数落在C组;
所以答案是:C;(2)根据(1)得出的数据补图如下:
【考点精析】利用频数分布直方图和扇形统计图对题目进行判断即可得到答案,需要熟知特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图);能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣4,2)、(1,﹣4),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以
 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的
 ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.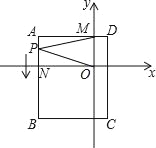
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣2)2+( )0﹣
)0﹣  ﹣(
﹣(  )﹣1;
)﹣1;
(2)[x(x2y2﹣xy)﹣y(x2﹣x3y)]÷x2y. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y=﹣2x与反比例函数y=
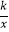 的图象相交于A(m,2),B两点.
的图象相交于A(m,2),B两点. 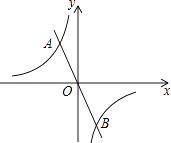
(1)求反比例函数的表达式及点B的坐标;
(2)结合图象直接写出当﹣2x>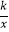 时,x的取值范围.
时,x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 已知a,b,c是三角形的三边,则a2+b2=c2
B. 在直角三角形中,两边的平方和等于第三边的平方
C. 在Rt△ABC中,∠
 ,所以a2+b2=c2
,所以a2+b2=c2D. 在Rt△ABC中,∠
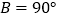 ,所以a2+b2=c2
,所以a2+b2=c2 -
科目: 来源: 题型:
查看答案和解析>>【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的概率是
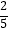 ;若往盒中再放进1个黑球,这时取得黑球的概率变为
;若往盒中再放进1个黑球,这时取得黑球的概率变为  .
.
(1)填空:x= , y=;
(2)小王和小林利用x个黑球和y个白球进行摸球游戏.约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在四边形ABCD中,∠A=90°,AD=6,AB=8,BC=26,CD=24
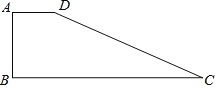
(1)求四边形ABCD的面积.
(2)求D到BC的距离.
相关试题

