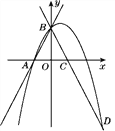
【题目】如图：已知抛物线与轴交于A、B两点（点A在点B左侧），与交于点C，抛物线对称轴与轴交于点D， 为轴上一点。

（1）写出点A、B、C的坐标（用表示）；

（2）若以DE为直径的圆经过点C且与抛物线交于另一点F，

①求抛物线解析式；

②P为线段DE上一动（不与D、E重合），过P作作，判断是否为定值，若是，请求出定值，若不是，请说明理由；

（3）如图②，将线段绕点顺时针旋转30°，与相交于点，连接.点是线段的中点，连接.若点是线段上一个动点，连接，将△绕点逆时针旋转得到△，延长交于点。若△的面积等于△的面积的，求线段的长．

参考答案：

【答案】（1）A(-3m，0)，B(m，0)，C(0， )

（2）①，② ，理由见解析；

（3）线段的长为2或

【解析】（1）A（-3m，0），B（m，0），C（0， ）

（2）△DCE为直角三角形．

①OC2=OD·OE，m=，∴

②∵DE为直径，∴∠DCE=∠DFE=90°，∵PQ⊥EC，PH⊥DF，∴PQ∥DC，PH∥EF， ，∴

（3）A（，0），B（，0），又∠OAM=60° ，∴cos30°=，∴OM=6，M（0，6）

又tan∠ABM==，∴∠OBM=60° ，∠AMB=90° ，

是线段的中点，∴∠OSM=60° ，∴∠AOS=30° ，又∠SOT=90° ，∠AOT=60° ，

∴直线TK：y=-x；BM：y=x-6，联立两个方程，解得：K（，-3）

设MN=a，TK=TO+OK=a+2，∴△KTN的高h=TK·sin60°=

NK=，∵S△KTN=S△ABM

， ∴

a=2或a=

关闭