【题目】E、F是线段AB上的两点,且AB=16,AE=1,BF=3,点G是线段EF上的一动点,分别以AG、BG为斜边在AB同侧作两个等腰直角三角形,直角顶点分别为D、C,如图所示,连接CD并取中点P,连结PG,点G从E点出发运动到F点,则线段PG扫过的图形面积为______.

参考答案:
【答案】36
【解析】
分别延长AD、BC相交于点H,连接PH,EH,FH,易证四边形DGCH为矩形,且P为矩形DGCH的对角线交点,即P为HG中点,过P作MN∥AB分别交EH、FH与M、N,所以MN为△HEF的中位线,即点P的运动轨迹即为MN,所以GP扫过的图形即为梯形MEFN,再根据已知线段求出梯形MEFN的面积即可.
解:分别延长AD、BC交于点H,连接PH,EH,FH,
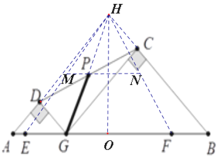
∵△ADG、△GCB为等腰直角三角形,
∴∠DGA=∠CGB=45°,
∴∠DGC=90°,
∴AH∥GC,
又∵∠HCG=90°,
∴∠HCG=∠DGC=90°,
∴DG∥HB,
∴四边形DGCH为矩形,
∵点P未DC中点,
∴点G、P、H三点共线,且P为HG的中点,
过P作MN∥于AB分别交EH、FH与M、N,
∴MN为△HEF的中位线,且MN即为点P的运动轨迹,
∴GP扫过的图形即为梯形MEFN,
∵AB=16,AE=1,BF=3,
∴EF=16-1-3=12,
∴![]() ,
,
过点H作HO垂直AB于O,
∴![]() ,
,
∴梯形的高为:![]() ,
,
∴![]() ,
,
即线段PG扫过的图形面积为36,
故答案为:36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
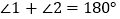 ,
,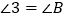 ,试判断
,试判断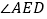 与
与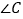 的大小关系,并证明你的结论。
的大小关系,并证明你的结论。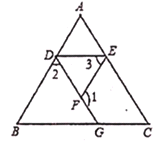
猜想:∠AED=∠C,
理由:∵∠2+∠ADF=180°( ),
∠1+∠2=180°( ),
∴∠1=∠ADF( ),
∴AD∥EF( ),
∴∠3=∠ADE( ),
∵∠3=∠B( ),
∴∠B=∠ADE( ),
∴DE∥BC( ),
∴∠AED=∠C( ), -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿EF折叠,使点C恰好落在AB边的中点C'上,点D落在D'处,C'D'交AE于点M.若AB=6,BC=9,求线段ED.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,对角线AC、BD交于点O,∠AOD=120°,E为BD上任意点,P为AE中点,则PO+PB的最小值为 ( )

A.
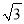 B.
B.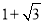 C.
C.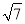 D.3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为研究学生的课余活动情况,采取抽样的方法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图(如图),请你根据图中提供的信息解答下列问题:


①这次调研,一共调查了 人.
②有阅读兴趣的学生占被调查学生总数的 %.
③有“其它”爱好的学生共多少人?
④补全折线统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小华就公众对在餐厅吸烟的态度进行了随机抽样调查,主要有四种态度:
A.顾客出面制止;B.劝说进吸烟室;C.餐厅老板出面制止;D.无所谓。
他将调查结果绘制了两幅不完整的统计图,请你根据图中的信息回答下列问题:

(1)这次抽样的样本容量是多少?
(2)请将统计图①补充完整。
(3)在统计图②中,求“无所谓”部分所对应的圆心角的度数。
相关试题

