【题目】如图,![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的大小关系,并证明你的结论。
的大小关系,并证明你的结论。
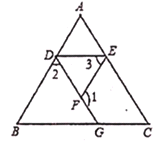
猜想:∠AED=∠C,
理由:∵∠2+∠ADF=180°( ),
∠1+∠2=180°( ),
∴∠1=∠ADF( ),
∴AD∥EF( ),
∴∠3=∠ADE( ),
∵∠3=∠B( ),
∴∠B=∠ADE( ),
∴DE∥BC( ),
∴∠AED=∠C( ),
参考答案:
【答案】见解析
【解析】
根据平行线的判定得出AD∥EF,得出∠B=∠ADE,得出DE∥BC,进而得出∠AED=∠C.
猜想:∠AED=∠C,
理由:∵∠2+∠ADF=180°(平角的定义),
∠1+∠2=180°(已知),
∴∠1=∠ADF(同角的补角相等),
∴AD∥EF(同位角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一根 24cm 的筷子,置于底面直径为 15cm,高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为 hcm,则 h 的取值范围是( )
A.h≤15cmB.h≥8cmC.8cm≤h≤17cmD.7cm≤h≤16cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=17,AC=10,高AD=8,则△ABC的周长是( )
A.54B.44C.36或48D.54或33
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,DC=2,点P是AB上的动点,则PC+PD的最小值为( )

A.8B.10C.12D.14
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿EF折叠,使点C恰好落在AB边的中点C'上,点D落在D'处,C'D'交AE于点M.若AB=6,BC=9,求线段ED.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,对角线AC、BD交于点O,∠AOD=120°,E为BD上任意点,P为AE中点,则PO+PB的最小值为 ( )

A.
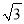 B.
B.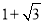 C.
C.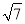 D.3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】E、F是线段AB上的两点,且AB=16,AE=1,BF=3,点G是线段EF上的一动点,分别以AG、BG为斜边在AB同侧作两个等腰直角三角形,直角顶点分别为D、C,如图所示,连接CD并取中点P,连结PG,点G从E点出发运动到F点,则线段PG扫过的图形面积为______.

相关试题

