【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

参考答案:
【答案】(1)证明见解析(2)菱形
【解析】
(1)根据正方形的性质和全等三角形的判定证明即可;
(2)四边形AECF是菱形,根据对角线垂直的平行四边形是菱形即可判断;
详证明:(1)∵四边形ABCD是正方形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABE=∠ADF,
在△ABE与△ADF中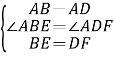 ,
,
∴△ABE≌△ADF.
(2)如图,连接AC,
四边形AECF是菱形.
理由:在正方形ABCD中,
OA=OC,OB=OD,AC⊥EF,
∴OB+BE=OD+DF,
即OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,对角线AC、BD交于点O,∠AOD=120°,E为BD上任意点,P为AE中点,则PO+PB的最小值为 ( )

A.
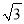 B.
B.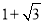 C.
C.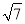 D.3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】E、F是线段AB上的两点,且AB=16,AE=1,BF=3,点G是线段EF上的一动点,分别以AG、BG为斜边在AB同侧作两个等腰直角三角形,直角顶点分别为D、C,如图所示,连接CD并取中点P,连结PG,点G从E点出发运动到F点,则线段PG扫过的图形面积为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为研究学生的课余活动情况,采取抽样的方法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图(如图),请你根据图中提供的信息解答下列问题:


①这次调研,一共调查了 人.
②有阅读兴趣的学生占被调查学生总数的 %.
③有“其它”爱好的学生共多少人?
④补全折线统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华就公众对在餐厅吸烟的态度进行了随机抽样调查,主要有四种态度:
A.顾客出面制止;B.劝说进吸烟室;C.餐厅老板出面制止;D.无所谓。
他将调查结果绘制了两幅不完整的统计图,请你根据图中的信息回答下列问题:

(1)这次抽样的样本容量是多少?
(2)请将统计图①补充完整。
(3)在统计图②中,求“无所谓”部分所对应的圆心角的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】只用无刻度的直尺作图(保留作图痕迹,不要求写作法)
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,其中四边形AEBF是平行四边形,请你在图中画出∠AOB的平分线.
(2)如图2,已知E是菱形ABCD中AB边上的中点,请你在图中画出一个矩形EFGH,使得其面积等于菱形ABCD的一半.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3
 、7
、7 、9
、9 ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2 、4
、4 、6
、6 、8
、8 ;盒子外有一张写着5
;盒子外有一张写着5 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
相关试题

