Question

【题目】如图①，A是线段BC上一点，△ABD和△ACE都是等边三角形．

(1)连结BE，DC，求证：BE＝DC.

(2)如图②，将△ABD绕点A顺时针旋转得到△AB′D′.

①当旋转角为__ _度时，边AD′落在AE上．

②在①的条件下，延长DD′交CE于点P，连结BD′，CD′.当线段AB，AC满足什么数量关系时，△BDD′与△CPD′全等？并给予证明．

Answer 1

【答案】(1)证明见解析(2)①60°②当AC＝2AB时，△BDD′与△CPD′全等

【解析】试题分析：（1）根据等边三角形的性质可得AB=AD，AE=AC，∠BAD=∠CAE=60°，然后求出∠BAE=∠DAC，再利用“边角边”证明△BAE和△DAC全等，根据全等三角形对应边相等即可得证；（2）①求出∠DAE，即可得到旋转角度数；②当AC=2AB时，△BDD′与△CPD′全等．根据旋转的性质可得AB=BD=DD′=AD′，利用SSS证得△ABD′≌△DBD′，可得∠ABD′=∠DBD′=30°，同理∠AD′B＝∠DD′B＝30°，所以DP∥BC.再证得∠DBD'=∠PCD'，BD'=CD'，∠DD'B=∠PD'C，然后利用“角边角”证明△BDD′≌△CPD′即可．

试题解析：

(1)∵△ABD和△ACE都是等边三角形．

∴AB＝AD，AE＝AC，∠BAD＝∠CAE＝60°，

∴∠BAD＋∠DAE＝∠CAE＋∠DAE，

即∠BAE＝∠DAC.

在△BAE和△DAC中，

∵

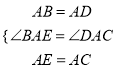
∴△BAE≌△DAC(SAS)．∴BE＝DC.

(2)①∵∠BAD＝∠CAE＝60°，

∴∠DAE＝180°－60°×2＝60°.

∵边AD′落在AE上，

∴旋转角＝∠DAE＝60°.

②当AC＝2AB时，△BDD′与△CPD′全等．

证明如下：

由旋转可知，AB′与AD重合，

∴AB＝DB＝DD′＝AD′.

又∵BD′＝BD′，∴△ABD′≌△DBD′(SSS)．

∴∠ABD′＝∠DBD′＝∠ABD＝×60°＝30°.

同理，∠AD′B＝∠DD′B＝30°，∴DP∥BC.

∵△ACE是等边三角形，

∴AC＝AE＝CE，∠ACE＝60°.

∵AC＝2AB，∴AE＝2AD′.

∴∠PCD′＝∠ACD′＝∠ACE＝×60°＝30°.

∴∠ABD′＝∠ACD′.∴BD′＝CD′.

∵DP∥BC，∴∠PD′C＝∠ACD′＝30°.

∴∠DBD′＝∠DD′B＝∠PCD′＝∠PD′C＝30°.

在△BDD′与△CPD′中，

∵

∴△BDD′≌△CPD′(ASA)．