Question

【题目】如图，AB是⊙O直径，点P是AB下方的半圆上不与点A，B重合的一个动点，点C为AP中点，延长CO交⊙O于点D，连接AD，过点D作⊙O的切线交PB的廷长线于点E，连CE．

（1）求证：△DAC≌△ECP；

（2）填空：

①当∠DAP= 时，四边形DEPC为正方形；

②在点P运动过程中，若⊙O半径为5，tan∠DCE=，则AD= ．

Answer 1

【答案】(1)详见解析；（2）①∠DAP=45°；②AD=4．

【解析】

试题分析：（1）先由切线的性质得到∠CDE=90°，再利用垂径定理的推理得到DC⊥AP，接着根据圆周角定理得到∠APB=90°，于是可判断四边形DEPC为矩形，所以DC=EP，然后根据“SAS”判断△DAC≌△ECP；（2）①利用四边形DEPC为矩形得到DE=PC=AC，则根据正方形的判定方法得DC=CP时，四边形DEPC为正方形，则DC=CP=AC，于是得到此时△ACD为等腰直角三角形，所以∠DAP=45°；②先证明∠ADC=∠DCE，再在Rt△ACD中利用正切得到tan∠ADC==，则设AC=x，DC=2x，利用勾股定理得到AD=x，然后在Rt△AOC中利用勾股定理得到x2+（2x﹣5）2=52，再解方程求出x即可得到AD的长．

试题解析：（1）证明：∵DE为切线，

∴OD⊥DE，

∴∠CDE=90°，

∵点C为AP的中点，

∴DC⊥AP，

∴∠DCA=∠DCP=90°，

∵AB是⊙O直径，

∴∠APB=90°，

∴四边形DEPC为矩形，

∴DC=EP，

在△DAC和△ECP中

，

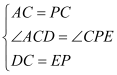∴△DAC≌△ECP；

（2）解：①∵四边形DEPC为矩形，

∵DE=PC=AC，

∵当DC=CP时，四边形DEPC为正方形，

此时DC=CP=AC，

∴△ACD为等腰直角三角形，

∴∠DAP=45°；

②∵DE=AC，DE∥AC，

∴四边形ACED为平行四边形，

∴AD∥CE，

∴∠ADC=∠DCE，

在Rt△ACD中，tan∠ADC==tan∠DCE=，

设AC=x，则DC=2x，

∴AD==x，

在Rt△AOC中，AO=5，OC=CD﹣OD=2x﹣5，

∴x2+（2x﹣5）2=52，解得x1=0（舍去），x2=4，

∴AD=4．