【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
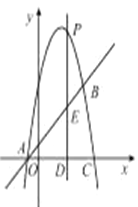
(1)求抛物线的解析式;
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 、点
、点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①当![]() 时,求
时,求![]() 点坐标;
点坐标;
② 是否存在点![]() 使
使![]() 为等腰三角形,若存在请直接写出点
为等腰三角形,若存在请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)y=﹣x2+4x+5;(2)①P点坐标为(2,9)或(6,﹣7);②(![]() ,
,![]() )或(4+
)或(4+![]() ,﹣4
,﹣4![]() ﹣8)或(4﹣
﹣8)或(4﹣![]() ,4
,4![]() ﹣8)或(0,5).
﹣8)或(0,5).
【解析】
试题分析:(1)由直线解析式可求得B点坐标,由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)①可设出P点坐标,则可表示出E、D的坐标,从而可表示出PE和ED的长,由条件可知到关于P点坐标的方程,则可求得P点坐标;
②由E、B、C三点坐标可表示出BE、CE和BC的长,由等腰三角形的性质可得到关于E点坐标的方程,可求得E点坐标,则可求得P点坐标.
试题解析:(1)∵点B(4,m)在直线y=x+1上,
∴m=4+1=5,
∴B(4,5),
把A、B、C三点坐标代入抛物线解析式可得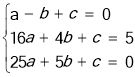 ,解得
,解得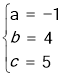 ,
,
∴抛物线解析式为y=﹣x2+4x+5;
(2)①设P(x,﹣x2+4x+5),则E(x,x+1),D(x,0),
则PE=|﹣x2+4x+5﹣(x+1)|=|﹣x2+3x+4|,DE=|x+1|,
∵PE=2ED,
∴|﹣x2+3x+4|=2|x+1|,
当﹣x2+3x+4=2(x+1)时,解得x=﹣1或x=2,但当x=﹣1时,P与A重合不合题意,舍去,
∴P(2,9);
当﹣x2+3x+4=﹣2(x+1)时,解得x=﹣1或x=6,但当x=﹣1时,P与A重合不合题意,舍去,
∴P(6,﹣7);
综上可知P点坐标为(2,9)或(6,﹣7);
②设P(x,﹣x2+4x+5),则E(x,x+1),且B(4,5),C(5,0),
∴BE=![]() |x﹣4|,CE=
|x﹣4|,CE=![]() ,BC=
,BC=![]() ,
,
当△BEC为等腰三角形时,则有BE=CE、BE=BC或CE=BC三种情况,
当BE=CE时,则![]() |x﹣4|=
|x﹣4|=![]() ,解得x=
,解得x=![]() ,此时P点坐标为(
,此时P点坐标为(![]() ,
,![]() );
);
当BE=BC时,则![]() |x﹣4|=
|x﹣4|=![]() ,解得x=4+
,解得x=4+![]() 或x=4﹣
或x=4﹣![]() ,此时P点坐标为(4+
,此时P点坐标为(4+![]() ,﹣4
,﹣4![]() ﹣8)或(4﹣
﹣8)或(4﹣![]() ,4
,4![]() ﹣8);
﹣8);
当CE=BC时,则![]() =
=![]() ,解得x=0或x=4,当x=4时E点与B点重合,不合题意,舍去,此时P点坐标为(0,5);
,解得x=0或x=4,当x=4时E点与B点重合,不合题意,舍去,此时P点坐标为(0,5);
综上可知存在满足条件的点P,其坐标为(![]() ,
,![]() )或(4+
)或(4+![]() ,﹣4
,﹣4![]() ﹣8)或(4﹣
﹣8)或(4﹣![]() ,4
,4![]() ﹣8)或(0,5).
﹣8)或(0,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义一种新运算“*”,规定a*b=ab+a﹣b,如1*3=1×3+1﹣3,则﹣2*5等于( )
A. 17B. 15C. ﹣17D. ﹣15
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根为0,则a的值为( )
A.1或﹣1
B.﹣1
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果 9x2+kx+25 是一个完全平方式,那么 k 的值是( )
A. 30 B. ±30 C. 15 D. ±15
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子中,属于最简二次根式的是( )
A.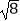
B.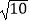
C.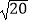
D.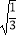
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,E是BC中点,P为BD上一动点,则PE+PC的最小值为( )
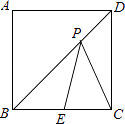
A.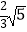
B.2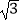
C.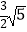
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知一次函数y=﹣
 x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
A.(0,3)
B.(0, )
)
C.(0, )
)
D.(0, )
)
相关试题

