【题目】苏科版九年级下册数学课本91页有这样一道习题:


(1)复习时,小明与小亮、数学老师交流了自己的两个见解,并得到了老师的认可:
①可以假定正方形的边长AB=4a,则AE=DE=2a,DF=a,利用“两边分别成比例且夹角相等的两个三角形相似”可以证明△ABE∽△DEF;请结合提示写出证明过程.
②图中的相似三角形共三对,而且可以借助于△ABE与△DEF中的比例线段来证明△EBF与它们相似.证明过程如下:

(2)交流之后,小亮尝试对问题进行了变化,在老师的帮助下,提出了新的问题,请你解答:
已知:如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连结FC.
(AB>AE)

①求证:△AEF∽△ECF;
②设BC=2,AB=a,是否存在a值,使得△AEF与△BFC相似.若存在,请求出a的值;若不存在,请说明理由.
参考答案:
【答案】(1)见解析;(2)①见解析;②当a=![]() 时,△AEF与△BFC相似
时,△AEF与△BFC相似
【解析】(1)按提示,列出条件,便得到相似三角形;
(2)![]() 由∠AEF=∠DCE,∠A=∠D=90°,可证△AEF∽△DEC,得
由∠AEF=∠DCE,∠A=∠D=90°,可证△AEF∽△DEC,得![]() ,再由AE=ED,得
,再由AE=ED,得![]() ,证得△AEF∽△EFC.
,证得△AEF∽△EFC.
②由题意得:AE=DE=1,由△AEF∽△DCE得:AF=![]() ,故BF=a-
,故BF=a-![]() .分两种情况:若△AEF∽△BFC则
.分两种情况:若△AEF∽△BFC则![]() ;若△AEF∽△BCF,则
;若△AEF∽△BCF,则![]() .分别求解可得.
.分别求解可得.
(1)①证明:假定正方形的边长AB=4a,则AE=DE=2a,DF=a,
在正方形ABCD中,∠A=∠D=90°.
![]() =2,∠A=∠D=90°.
=2,∠A=∠D=90°.
∴△ABE∽△DEF.
(2)①证明:∵∠D=90°,∴∠D EC+∠DCE=90°
∵EF⊥EC,∴∠D EC+∠AEF=90°
∴∠AEF=∠DCE,又因为∠A=∠D=90°
∴△AEF∽△DEC
∴![]() ,∵AE=ED,
,∵AE=ED,
∴![]() ,即
,即![]() ,∵∠A=∠BEF=90°
,∵∠A=∠BEF=90°
∴△AEF∽△EFC.
②由题意得:AE=DE=1,由△AEF∽△DCE得:AF=![]() ,故BF=a-
,故BF=a-![]() .
.
若△AEF∽△BFC
则![]() ,此时a无解;
,此时a无解;
若△AEF∽△BCF
则![]() ,此时a=
,此时a=![]() .
.
所以,当a=![]() 时,△AEF与△BFC相似.
时,△AEF与△BFC相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+
 x+c(a≠0)与x轴交于点A,B两点,
x+c(a≠0)与x轴交于点A,B两点,其中A(-1,0),与y轴交于点C(0,2).
(1)求抛物线的表达式及点B坐标;
(2)点E是线段BC上的任意一点(点E与B、C不重合),过点E作平行于y轴的直线交抛物线于点F,交x轴于点G.
①设点E的横坐标为m,用含有m的代数式表示线段EF的长;
②线段EF长的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□
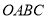 的顶点
的顶点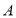 的坐标为
的坐标为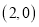 ,
,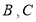 在第一象限反比例函数
在第一象限反比例函数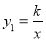 和
和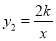 的图象分别经过
的图象分别经过 两点,延长
两点,延长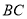 交
交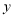 轴于点
轴于点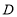 . 设
. 设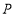 是反比例函数
是反比例函数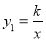 图象上的动点,若
图象上的动点,若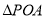 的面积是
的面积是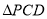 面积的2倍,
面积的2倍,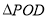 的面积等于
的面积等于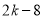 ,则
,则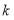 的值为________。
的值为________。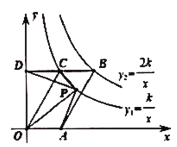
-
科目: 来源: 题型:
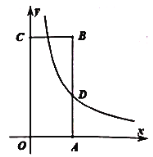
查看答案和解析>>【题目】如图,矩形
 放置在平面直角坐标系上,点
放置在平面直角坐标系上,点 分别在
分别在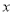 轴,
轴,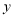 轴的正半轴上,点
轴的正半轴上,点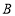 的坐标是
的坐标是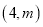 ,其中
,其中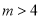 ,反比例函数y=
,反比例函数y=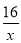
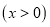 的图象交
的图象交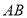 交于点
交于点 .
. 
(1)
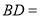 _____(用
_____(用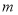 的代数式表示)
的代数式表示) (2)设点
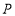 为该反比例函数图象上的动点,且它的横坐标恰好等于
为该反比例函数图象上的动点,且它的横坐标恰好等于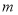 ,连结
,连结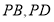 .
. ①若
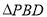 的面积比矩形
的面积比矩形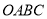 面积多8,求
面积多8,求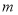 的值。
的值。②现将点
 绕点
绕点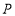 逆时针旋转
逆时针旋转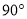 得到点
得到点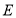 ,若点
,若点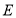 恰好落在
恰好落在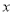 轴上,直接写出
轴上,直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
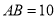 ,
,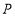 是线段
是线段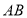 上的一个动点,分别以
上的一个动点,分别以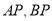 为边,在
为边,在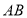 的同侧构造菱形
的同侧构造菱形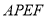 和菱形
和菱形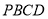 ,
,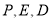 三点在同一条直线上连结
三点在同一条直线上连结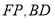 ,设射线
,设射线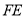 与射线
与射线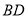 交于
交于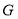 .
. 
(1)当
 在点
在点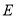 的右侧时,求证:四边形
的右侧时,求证:四边形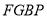 是平形四边形.
是平形四边形.(2)连结
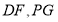 ,当四边形
,当四边形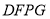 恰为矩形时,求
恰为矩形时,求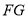 的长.
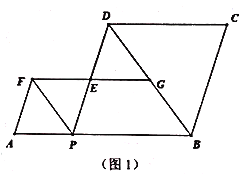
的长. (3)如图2,设
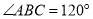 ,
,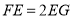 ,记点
,记点 与
与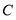 之间的距离为
之间的距离为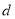 ,直接写出
,直接写出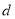 的所有值.
的所有值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A,B在圆上,BC,AD分别与该圆相交于点E,F,G是弧AF的三等分点(弧AG>弧GF),BG交AF于点H.若弧AB的度数为30°,则∠GHF等于( )
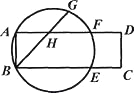
A. 40° B. 45° C. 55° D. 80°
相关试题

