【题目】已知△ABC是等腰三角形,且∠A=40°,那么∠ACB的外角的度数是
A. 110° B. 140° C. 110°或140° D. 以上都不对
参考答案:
【答案】D
【解析】
利用等腰三角形的性质,得到两底角相等,结合三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和,可直接得到结果.
解:∵等腰三角形两底角相等,三角形的任一外角等于和它不相邻的两个内角之和,
∴当顶角∠A=40°时,则∠ACB=∠B=![]() (180°-40
(180°-40![]() )=70°,
)=70°,
∴∠ACB的外角的度数是180°-70°=110°,
∴当底角∠A=40°时,∠B=40°,则∠ACB的外角的度数为2∠A=2×40![]() =80°,
=80°,
当底角∠A=40°时,∠ACB=40°,则∠ACB的外角的度数为180![]() -40
-40![]() =140°.
=140°.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题,
例如:∵
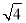 <
<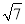 <
<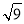 ,即2<
,即2<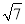 <3,∴
<3,∴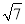 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(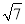 ﹣2).
﹣2).请解答:(1)
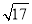 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .(2)已知:5﹣
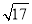 小数部分是m,6+
小数部分是m,6+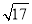 小数部分是n,且(x+1)2=m+n,请求出满足条件的x的值.
小数部分是n,且(x+1)2=m+n,请求出满足条件的x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
-
科目: 来源: 题型:
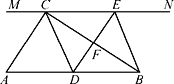
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在安庆市第三届中小学生道路交通安全网络知识竞赛活动中,某中学的老师要求同学们都参加社会实践活动,一天,王明和张强两位同学到市中心的广场的十字路口,观察、统计上午7:
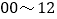 :00中闯红灯的人次,制作了如下的两个数据统计图
:00中闯红灯的人次,制作了如下的两个数据统计图 井且提出了一些问题
井且提出了一些问题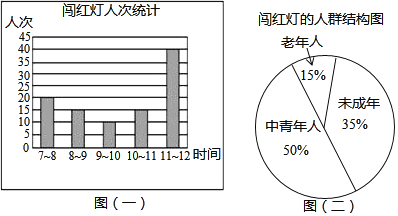
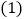 求图
求图 一
一 提供的五个数据
提供的五个数据 各时段闯红灯人次
各时段闯红灯人次 的平均数
的平均数 并说明这两幅统计图各有什么特点?
并说明这两幅统计图各有什么特点? 估计一个月
估计一个月 按30天计算
按30天计算 上午7:
上午7: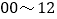 :00在该十字路口闯红灯的未成年人约有多少人次?
:00在该十字路口闯红灯的未成年人约有多少人次?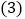 请你根据统计图提供的信息向交通管理部门提出一条合理化建议.
请你根据统计图提供的信息向交通管理部门提出一条合理化建议. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.

(1)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.
(2)若DC=2,求证:△ABD≌△DCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,O为AC中点,点P在AC上,若OP=
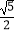 ,tan∠A=
,tan∠A=  ,∠B=120°,BC=2
,∠B=120°,BC=2 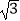 ,则AP= .
,则AP= .
相关试题

