【题目】阅读下面的文字,解答问题,
例如:∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2).
﹣2).
请解答:(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)已知:5﹣![]() 小数部分是m,6+
小数部分是m,6+![]() 小数部分是n,且(x+1)2=m+n,请求出满足条件的x的值.
小数部分是n,且(x+1)2=m+n,请求出满足条件的x的值.
参考答案:
【答案】(1)4 ,![]() ;(2)x=0或-2.
;(2)x=0或-2.
【解析】
(1)根据夹逼法可求![]() 的整数部分和小数部分;
的整数部分和小数部分;
(2)首先估算出m,n的值,进而得出m+n的值,可求满足条件的x的值.
(1)∵4<![]() <5,
<5,
∴![]() 的整数部分是4,小数部分是
的整数部分是4,小数部分是![]() 4.
4.
故答案为:4;![]() ;
;
(2)∵5﹣![]() 小数部分是m,0<5﹣
小数部分是m,0<5﹣![]() <1,6+
<1,6+![]() 小数部分是n
小数部分是n
∴m=5-![]() , n=6+
, n=6+![]() -10=
-10=![]() -4
-4
∴m+n=1
∴(x+1)2=1
x+1=±1
解得:x=0或-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
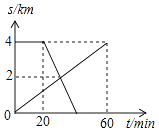
A.8:30
B.8:35
C.8:40
D.8:45 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
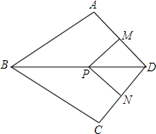
(1)求证:ADB=CDB;
(2)若ADC=90°,求证:四边形MPND是正方形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
-
科目: 来源: 题型:
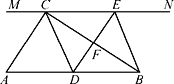
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰三角形,且∠A=40°,那么∠ACB的外角的度数是
A. 110° B. 140° C. 110°或140° D. 以上都不对
相关试题

