【题目】已知△ABC,O为AC中点,点P在AC上,若OP= ![]() ,tan∠A=
,tan∠A= ![]() ,∠B=120°,BC=2
,∠B=120°,BC=2 ![]() ,则AP= .
,则AP= .
参考答案:
【答案】2 ![]() 或
或 ![]()
【解析】解:作CD⊥AB的延长线于D,
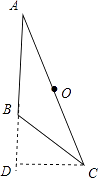
∵∠ABC=120°,
∴∠CBD=60°,
∵BC=2 ![]() ,
,
∴DC=BCsin60°=2 ![]()
![]() =3,
=3,
∵tan∠A= ![]() ,
,
∴AD=6,
∴AC= ![]() =3
=3 ![]() ,
,
∴AO= ![]() ,
,
∵OP= ![]() ,
,
∴AP=2 ![]() 或
或 ![]() .
.
所以答案是2 ![]() 或
或 ![]() .
.
【考点精析】根据题目的已知条件,利用解直角三角形的相关知识可以得到问题的答案,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰三角形,且∠A=40°,那么∠ACB的外角的度数是
A. 110° B. 140° C. 110°或140° D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】在安庆市第三届中小学生道路交通安全网络知识竞赛活动中,某中学的老师要求同学们都参加社会实践活动,一天,王明和张强两位同学到市中心的广场的十字路口,观察、统计上午7:
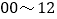 :00中闯红灯的人次,制作了如下的两个数据统计图
:00中闯红灯的人次,制作了如下的两个数据统计图 井且提出了一些问题
井且提出了一些问题
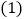 求图
求图 一
一 提供的五个数据
提供的五个数据 各时段闯红灯人次
各时段闯红灯人次 的平均数
的平均数 并说明这两幅统计图各有什么特点?
并说明这两幅统计图各有什么特点? 估计一个月
估计一个月 按30天计算
按30天计算 上午7:
上午7: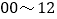 :00在该十字路口闯红灯的未成年人约有多少人次?
:00在该十字路口闯红灯的未成年人约有多少人次? 请你根据统计图提供的信息向交通管理部门提出一条合理化建议.
请你根据统计图提供的信息向交通管理部门提出一条合理化建议. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.

(1)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.
(2)若DC=2,求证:△ABD≌△DCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AEAF=
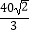 ,则EF的长为 .
,则EF的长为 . 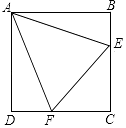
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为 .
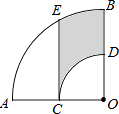
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点A、B在小正方形的顶点上.
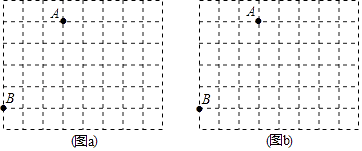
(1)在图a中画出△ABC(点C在小正方形的顶点上),使△ABC是等腰三角形且△ABC为钝角三角形;
(2)在图b中画出△ABD(点D在小正方形的顶点上),使△ABD是等腰三角形,且tan∠ABD=1.
相关试题

