【题目】如图,在△ABC 中,AB=AC,点D,E在边BC上,且BD=CE.
(1)求证: △ABD≌△ACE;
(2)若∠B=40°,AB=BE,求∠DAE的度数.

参考答案:
【答案】(1)见解析;(2)40°.
【解析】
(1)根据SAS即可证明.
(2)由AB=BE,推出∠BAE=∠BEA,由∠B=40°,推出∠BAE=∠BEA=70°,由△ABD≌△ACE,推出AD=AE,推出∠ADE=∠AED=70°,推出∠DAE=180°-70°-70°=40°.
(1)证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,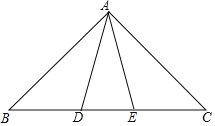
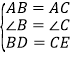 ,
,
∴△ABD≌△ACE.
(2)∵AB=BE,
∴∠BAE=∠BEA,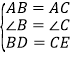
∵∠B=40°,
∴∠BAE=∠BEA=70°,
∵△ABD≌△ACE,
∴AD=AE,
∴∠ADE=∠AED=70°,
∴∠DAE=180°70°70°=40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )

A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.
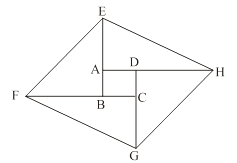
(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C  在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,∠B= ∠D,∠C=
∠D,∠C=  ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;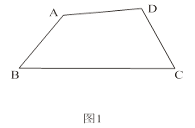
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.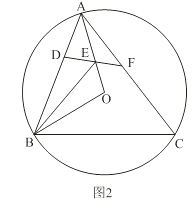
求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当DH=BG时,求△BGH与△ABC的面积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,
, 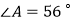 .以
.以  为直径的
为直径的  交
交  于点
于点  ,
,  是
是  上一点,且
上一点,且 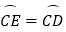 ,连接
,连接 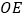 ,过点
,过点  作
作 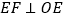 ,交
,交  的延长线于点
的延长线于点 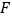 ,则
,则  的度数为( )
的度数为( )
A.
B.
C.
D.
相关试题

