【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() .以
.以 ![]() 为直径的
为直径的 ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() 是
是 ![]() 上一点,且
上一点,且 ![]() ,连接
,连接 ![]() ,过点
,过点 ![]() 作
作 ![]() ,交
,交 ![]() 的延长线于点
的延长线于点 ![]() ,则
,则 ![]() 的度数为( )
的度数为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】解:在RtΔΑΒC中,∠ΑCΒ=90°, ∠Α = 56 °,
所以 ∠ABC=90°-56°=34°.
因为弧CE=弧CD,
所以∠COE=2∠ABC=68°.
在四边形OCFE中,
因为OC⊥AF,OE⊥EF,
所以∠F=180°-∠COE=180°-68°=112°。
故选C。
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,点D,E在边BC上,且BD=CE.
(1)求证: △ABD≌△ACE;
(2)若∠B=40°,AB=BE,求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,∠B= ∠D,∠C=
∠D,∠C=  ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;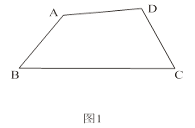
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.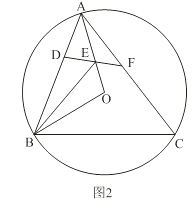
求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当DH=BG时,求△BGH与△ABC的面积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,
中, 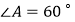 ,
, 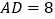 ,
, 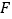 是
是  的中点.过点
的中点.过点 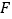 作
作 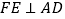 ,垂足为
,垂足为 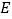 .将
.将 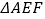 沿点
沿点 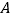 到点
到点 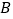 的方向平移,得到
的方向平移,得到  .设
.设 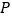 、
、 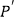 分别是
分别是 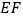 、
、 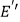 的中点,当点
的中点,当点 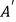 与点
与点 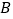 重合时,四边形
重合时,四边形 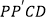 的面积为( )
的面积为( )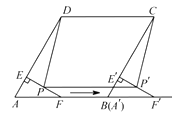
A.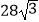
B.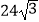
C.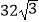
D.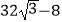
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
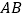 是
是 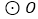 的直径,
的直径, 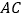 是弦,
是弦, 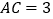 ,
, 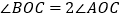 .若用扇形
.若用扇形  (图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是 .
(图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是 . 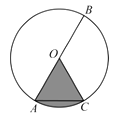
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一笔直的沿湖道路
 上有
上有  、
、 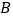 两个游船码头,观光岛屿
两个游船码头,观光岛屿 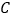 在码头
在码头  北偏东
北偏东 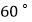 的方向,在码头
的方向,在码头 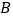 北偏西
北偏西  的方向,
的方向, 
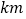 .游客小张准备从观光岛屿
.游客小张准备从观光岛屿 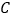 乘船沿
乘船沿  回到码头
回到码头  或沿
或沿  回到码头
回到码头 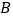 ,设开往码头
,设开往码头  、
、 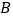 的游船速度分别为
的游船速度分别为 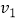 、
、  ,若回到
,若回到  、
、 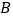 所用时间相等,则
所用时间相等,则  (结果保留根号).
(结果保留根号).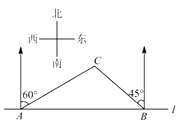
相关试题

