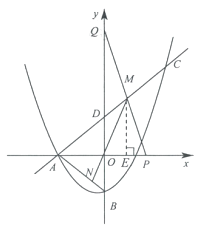
【题目】如图,抛物线 ![]() 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C ![]() 在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示).
参考答案:
【答案】
(1)
解:把点C(6,![]() )代入抛物线得:
)代入抛物线得:![]() =9+
=9+![]() +c.
+c.
解得c=-3.
当y=0时,![]() x2+
x2+![]() x-3=0.
x-3=0.
解得:x1=-4,x2=3.
∴A(-4,0).
设直线AC的函数表达式为:y=kx+b(k≠0).
把A(-4,0),C(6,![]() )代入得:
)代入得:
![]()
解得:![]()
∴直线AC的函数表达式为:y=![]() x+3.
x+3.
(2)
①证明:∵在Rt△AOB中,tan∠OAB=![]() =
=![]() .
.
在Rt△AOB中,tan∠OAD=![]() =
=![]() .
.
∴∠OAB=∠OAD.
∵在Rt△POQ中,M为PQ中点.
∴OM=MP.
∴∠MOP=∠MPO.
又 ∵∠MOP=∠AON.
∴∠APM=∠AON.
∴△APM∽△AON.
②解:如下图,过点M作ME⊥x轴于点E.
∵OM=MP.
∴OE=EP.
又∵点M的横坐标为m.
∴AE=m+4,AP=2m+4.
∵tan∠OAD=![]() .
.
∴cos∠EAM=cos∠OAD=![]() .
.
∴AM=![]() AE=
AE=![]() .
.
∵△APM∽△AON.
∴![]() =
=![]() .
.
∴AN=![]() =
=![]() .
.
【解析】(1)把点C(6,![]() )代入抛物线求出c的值,令y=0求出A点坐标,再用待定系数法求出直线AC的函数表达式.
)代入抛物线求出c的值,令y=0求出A点坐标,再用待定系数法求出直线AC的函数表达式.
(2)①在Rt△AOB中,tan∠OAB=![]() =
=![]() . 在Rt△AOB中,tan∠OAD=
. 在Rt△AOB中,tan∠OAD=![]() =
=![]() .从而得出∠OAB=∠OAD;在Rt△POQ中,M为PQ中点得出OM=MP.∠APM=∠AON;从而证明△APM∽△AON.
.从而得出∠OAB=∠OAD;在Rt△POQ中,M为PQ中点得出OM=MP.∠APM=∠AON;从而证明△APM∽△AON.
②如上图,过点M作ME⊥x轴于点E;由OM=MP.得出OE=EP;点M的横坐标为m;得出AE=m+4,AP=2m+4.
根据tan∠OAD=![]() .求出cos∠EAM=cos∠OAD=
.求出cos∠EAM=cos∠OAD=![]() ;再根据△APM∽△AON;得出AN=
;再根据△APM∽△AON;得出AN=![]() =
=![]() .
.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为10,B是数轴上位于点A左侧一点,且AB=30,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为
 秒.
秒.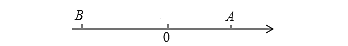
(1)数轴上点B表示的数是________,点P表示的数是________(用含
 的代数式表示);
的代数式表示);(2)若M为线段AP的中点,N为线段BP的中点,在点P运动的过程中,线段MN的长度会发生变化吗?如果不变,请求出这个长度;如果会变化,请用含
 的代数式表示这个长度;
的代数式表示这个长度;(3)动点Q从点B处出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时与点Q相距4个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )

A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.
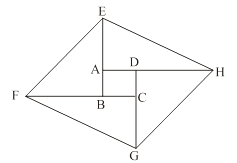
(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,点D,E在边BC上,且BD=CE.
(1)求证: △ABD≌△ACE;
(2)若∠B=40°,AB=BE,求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,∠B= ∠D,∠C=
∠D,∠C=  ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.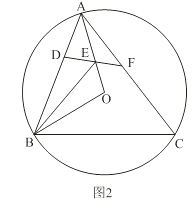
求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当DH=BG时,求△BGH与△ABC的面积之比.
相关试题

