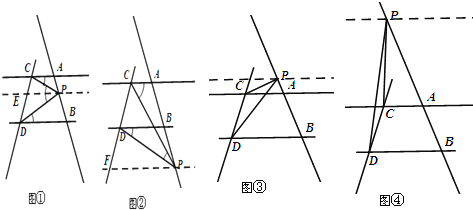
【题目】如图,已知直线AC∥BD,直线AB,CD不平行,点P在直线AB上,且和点A、B不重合.

(1)如图①,当点P在线段AB上时,若∠PCA=20°,∠PDB=30°,求∠CPD的度数;
(2)当点P在A、B两点之间运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)
(3)如图②,当点P在线段AB延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?并说明理由.
(4)当点P在线段BA延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)
参考答案:
【答案】(1)50°;(2)∠CPD=∠PCA+∠PDB;(3)∠CPD=∠CPF﹣∠DPF=∠PCA﹣∠PDB;(4)见解析
【解析】
试题分析:(1)如图①,过P点作PE∥AC交CD于E点,由于AC∥BD,则PE∥BD,根据平行线的性质得∠CPE=∠PCA=20°,∠DPE=∠PDB=30°,所以∠CPD=50°;
(2)证明方法与(1)一样;
(3)如图②,过P点作PF∥BD交CD于F点,由于AC∥BD,则PF∥AC,根据平行线的性质得∠CPF=∠PCA,∠DPF=∠PDB,所以∠CPD=∠PCA﹣∠PDB;
(4)如图③和④,类似(3)的说明方法易得∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系.
解:(1)如图①,过P点作PE∥AC交CD于E点,
∵AC∥BD
∴PE∥BD,
∴∠CPE=∠PCA=20°,∠DPE=∠PDB=30°,
∴∠CPD=∠CPE+∠DPE=50°;
(2)∠CPD=∠PCA+∠PDB(证明方法与(1)一样;
(3)∠CPD=∠PCA﹣∠PDB.理由如下:
如图②,过P点作PF∥BD交CD于F点,
∵AC∥BD,
∴PF∥AC,
∴∠CPF=∠PCA,∠DPF=∠PDB,
∴∠CPD=∠CPF﹣∠DPF=∠PCA﹣∠PDB;
(4)如图③,∠CPD=∠PDB﹣∠PCA;
如图④,∠CPD=∠PCA﹣∠PDB.
(证明方法与(3)类似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(a﹣1,b﹣2)关于x轴对称与关于y轴对称的点坐标相同,则P点坐标为( )
A. (﹣1,﹣2) B. (﹣1,0) C. (0,﹣2) D. (0,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2ax2﹣8a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠BAC=90,D是BC的中点,E是AD的中点,过点A作AF//BC交BE的延长线于点F
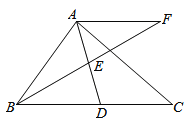
(1)求证:△AEF≌△DEB;
(2)证明:四边形ADCF是菱形;
(3)若AB=4,AC=5,求菱形ADCF的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中, A(0,4),B(-3,0).
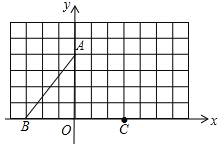
(1)①画出线段AB关于y轴对称线段AC;
②将线段AC绕点C顺时针旋转一个角,得到对应线段CD,使得AD//x轴,请画出线段CD;
(2)判断四边形ABCD的形状 ;
(3)若直线
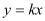 平分四边形ABCD的面积,请直接写出实数k的值.
平分四边形ABCD的面积,请直接写出实数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】64的立方根是( )
A.4
B.±4
C.8
D.±8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x,-4)与点B(3,y)关于x轴对称,那么x+y的值为________.
相关试题

