【题目】在Rt△ABC中,∠BAC=90,D是BC的中点,E是AD的中点,过点A作AF//BC交BE的延长线于点F
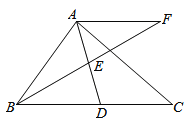
(1)求证:△AEF≌△DEB;
(2)证明:四边形ADCF是菱形;
(3)若AB=4,AC=5,求菱形ADCF的面积。
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)10.
【解析】
试题分析:(1)根据AAS证明即可判定.
(2)先证明四边形ADCF是平行四边形,再证明DA=DC即可.
(3)利用S菱形ADCF=2S△ADC=S△ABC即可求解.
试题解析:(1)∵AF∥BD,
∴∠AFE=∠DBE,
∵E是AD中点,
∴AE=ED,
在△BDE和△FAE中,
 ,
,
∴△AFE≌△DBE.
(2)连接CF.

∵△AFE≌△DBE,
∴AF=BD
∵∠BAC=90°,BD=CD,
∴AD=DC=DB,
∴AF∥CD,AF=DC,
∴四边形ADCF是平行四边形,
∵DA=CD,
∴四边形ADCF是菱形.
(3)∵S△ABC=![]() ×AB×AC=10,
×AB×AC=10,
∵四边形ADCF是菱形,BD=DC,S△ABC=2S△ADC,
∴S菱形ADCF=2S△ADC=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形是轴对称图形,其对称轴是_______________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(a﹣1,b﹣2)关于x轴对称与关于y轴对称的点坐标相同,则P点坐标为( )
A. (﹣1,﹣2) B. (﹣1,0) C. (0,﹣2) D. (0,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2ax2﹣8a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AC∥BD,直线AB,CD不平行,点P在直线AB上,且和点A、B不重合.

(1)如图①,当点P在线段AB上时,若∠PCA=20°,∠PDB=30°,求∠CPD的度数;
(2)当点P在A、B两点之间运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)
(3)如图②,当点P在线段AB延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?并说明理由.
(4)当点P在线段BA延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中, A(0,4),B(-3,0).
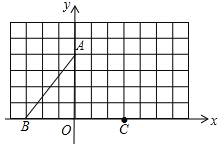
(1)①画出线段AB关于y轴对称线段AC;
②将线段AC绕点C顺时针旋转一个角,得到对应线段CD,使得AD//x轴,请画出线段CD;
(2)判断四边形ABCD的形状 ;
(3)若直线
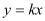 平分四边形ABCD的面积,请直接写出实数k的值.
平分四边形ABCD的面积,请直接写出实数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】64的立方根是( )
A.4
B.±4
C.8
D.±8
相关试题

