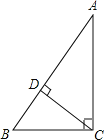
【题目】如图,在△ABC中,∠ACB=90,CD⊥AB,BC=1.
(1)如果∠BCD=30,求AC;
(2)如果tan∠BCD=![]() ,求CD.
,求CD.
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】(1)根据直角三角形的两锐角互余,由∠BCD的度数求出∠B的度数,利用锐角三角函数定义表示出tanB,将tanB及BC的长代入,即可求出AC的长;
(2)在直角三角形BDC中,由已知tan∠BCD的值,利用锐角三角函数定义得出BD与CD的比值为1:3,根据比值设出BD=k,CD=3k,再由BC的长,利用勾股定理列出关于k的方程,求出方程的解得到k的值,即可求出CD的长.
解:(1)∵CD⊥AB,∴∠BDC=90°.
∵∠DCB=30°,∴∠B=60°.
在Rt△ACB中,∠ACB=90°,∴tan60°=![]() .
.
∵BC=1,∴![]() ,则AC=
,则AC=![]() .
.
(2)在Rt△BDC中,tan∠BCD=![]() .
.
设BD=k,则CD=3k,
又BC=1,由勾股定理得:k2+(3k)2=1,解得:k=![]() 或k=
或k= ![]() (舍去).
(舍去).
∴CD=3k=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地某月1~20日中午12时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17 20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整:
气温分组
划记
频数
12≤x<17
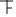
3
17≤x<22

10
22≤x<27

5
27≤x<32

2

(2)补全频数分布直方图;
(3)根据频数分布表或频数分布直方图,分析数据的分布情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.(
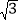 取1.73,结果保留整数.)
取1.73,结果保留整数.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
某中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地校参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆)
载客量
租金(元)
A
x
45x
400x
B
5-x
(2)若要保证租车费用不超过1900元,求x的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在干燥的路面上,使车子停止前进所需的刹车距离s(m)与车速v(km/h)的关系是s=
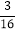 v+
v+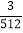 v2 .
v2 .(1)当v分别是48,64时,求相应的刹车距离s的值;
(2)司机小李正以72km/h的速度行驶,突然发现前方大约60m处有一不明障碍物,他立即刹车,车会撞上障碍物吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,拦水坝的横断面为梯形ABCD,坝顶宽AD=5米,斜坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
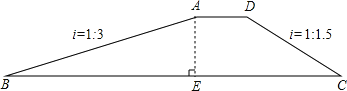
(1)求斜坡AB的长;
(2)求拦水坝的横断面梯形ABCD的周长.(注意:本题中的计算过程和结果均保留根号)
-
科目: 来源: 题型:
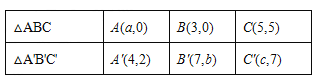
查看答案和解析>>【题目】已知△A'B'C'是由△ABC经过平移得到的,它们的顶点在平面直角坐标系中的坐标如下表所示:
(1)观察表中各对应点坐标的变化,并填空:
a= , b= ,c= ;
(2)在平面直角坐标系中画出△ABC及平移后的△A'B'C';(3)△A'B'C'的面积是 .
相关试题

