搜索
【题目】如图，已知∠BOC＝2∠AOC，OD平分∠AOB，∠BOE＝90°，若∠AOC＝40°，则∠DOE的度数等于（ ）
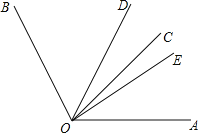
A.20°B.25°C.30°D.30°
参考答案：
【答案】C
【解析】
由∠BOC=2∠AOC可得∠AOB=3∠AOC=120°，由OD平分∠AOB可得∠AOD=
∠AOB=60°，由∠BOE=90°可得∠AOE=∠AOB-∠BOE=30°，所以∠DOE=∠AOD-∠AOE=30°．
解：∵∠BOC＝2∠AOC，∠AOC＝40°，
∴∠AOB＝∠BOC+∠AOC =3∠AOC＝120°，
∵∠BOE＝90°，
∴∠AOE＝∠AOB-∠BOE=30°，
∵OD平分∠AOB，
∴∠AOD＝
＝60°，
∴∠DOE＝∠AOD﹣∠AOE＝30°．
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点．
（1）求该抛物线的解析式；
（2）设（1）题中的抛物线上有一个动点P，当点P在抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标；
（3）设（1）题中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数a在数轴上表示的点在原点左侧，距离原点3个单位长，b在数轴上表示的点在原点右侧，距离原点2个单位长，c和d互为倒数，m与n互为相反数，y为最大的负整数，求（y+b）2+m（a-cd）-nb2的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知：Rt△ABC中，∠ACB=90°.作∠BAC的平分线AM交BC于点D，在所作图形中，将Rt△ABC沿某条直线折叠，使点A与点D重合，折痕EF交AC于点E，交AB于点F，连接DE、DF，再展回到原图形，得到四边形AEDF.
（1）试判断四边形AEDF的形状，并证明；
（2）若AB=10，BC=8，在折痕EF上有一动点P，求PC+PD的最小值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有24个小圆，…则第n个图形有__个小圆．
-
科目： 来源： 题型：
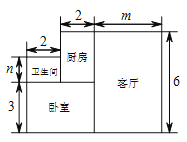
查看答案和解析>>【题目】小王购买了一套一居室，他准备将房子的地面铺上地砖，地面结构如图所示，根据图中所给的数据（单位：米），解答下列问题：
（1）用含
的代数式表示地面的总面积 
；
（2）已知
，且客厅面积是卫生间面积的 
倍，如果铺 
平方米地砖的平均费用为 
元，那么小王铺地砖的总费用为多少元? -
科目： 来源： 题型：
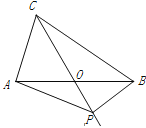
查看答案和解析>>【题目】如图，在△ABC中，AB=BC=4，AO=BO,P是射线CO上的一个动点，∠AOC=60°,则当△PAB为直角三角形时，AP的长为 __________________.
相关试题
