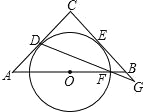
【题目】如图,已知△ABC,AC=BC,∠C=90°.O是AB的中点,⊙O与AC,BC分别相切于点D与点E.点F是⊙O与AB的一个交点,连DF并延长交CB的延长线于点G.则∠CDG= ,若AB=![]() ,则BG= .
,则BG= .
参考答案:
【答案】67.5°,2![]() ﹣2.
﹣2.
【解析】
试题解析:连接OD.
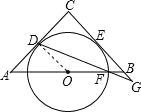
∵CD切⊙O于点D,
∴∠ODA=90°,∠DOA=45°,
∵OD=OF,
∴∠ODF=∠OFD=![]() ∠DOA=22.5°,
∠DOA=22.5°,
∴∠CDG=∠CDO﹣∠ODF=90°﹣22.5°=67.5°.
∵AC为圆O的切线,
∴OD⊥AC,
又O为AB的中点,∴AO=BO=![]() AB=2
AB=2![]() ,
,
∴圆的半径DO=FO=AOsinA=2![]() ×
×![]() =2,
=2,
∴BF=OB﹣OF=2![]() ﹣2.
﹣2.
∵GC⊥AC,OD⊥AC,
∴OD∥CG,
∴∠ODF=∠G,又∠OFD=∠BFG,
∴△ODF∽△BGF,
∴![]() ,即
,即![]()
∴BG=2![]() ﹣2.
﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(-2a2) ·(3ab2-5ab3)结果是( )
A. 6a3b2+10a3b3B. -6a3b2+10a2b3C. -6a3b2+10a3b3D. 6a3b2-10a3b3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知3×27×39=3x+8,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据有关测定,当气温处于人体正常体温(37℃)的黄金比值时,人体感到最舒适,则这个气温约为_________℃(结果保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长
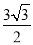 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.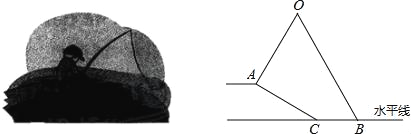
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数的乘除混合运算:有理数的乘除是同级运算,应按从________到________的顺序进行.
相关试题

