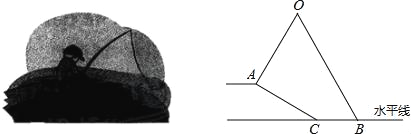
【题目】小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长![]() 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
参考答案:
【答案】浮漂B与河堤下端C之间的距离为1.5米.
【解析】
试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出∠CAD=180°﹣∠ODB﹣∠ACD=90°,解Rt△ACD,得出AD=ACtan∠ACD=![]() 米,CD=2AD=3米,
米,CD=2AD=3米,
再证明△BOD是等边三角形,得到BD=OD=OA+AD=4.5米,然后根据BC=BD﹣CD即可求出浮漂B与河堤下端C之间的距离.
试题解析:延长OA交BC于点D.

∵AO的倾斜角是60°,
∴∠ODB=60°.
∵∠ACD=30°,
∴∠CAD=180°﹣∠ODB﹣∠ACD=90°.
在Rt△ACD中,AD=ACtan∠ACD=![]() (米),
(米),
∴CD=2AD=3米,
又∵∠O=60°,
∴△BOD是等边三角形,
∴BD=OD=OA+AD=3+![]() =4.5(米),
=4.5(米),
∴BC=BD﹣CD=4.5﹣3=1.5(米).
答:浮漂B与河堤下端C之间的距离为1.5米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据有关测定,当气温处于人体正常体温(37℃)的黄金比值时,人体感到最舒适,则这个气温约为_________℃(结果保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AC=BC,∠C=90°.O是AB的中点,⊙O与AC,BC分别相切于点D与点E.点F是⊙O与AB的一个交点,连DF并延长交CB的延长线于点G.则∠CDG= ,若AB=
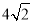 ,则BG= .
,则BG= .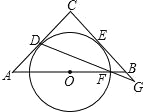
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数的乘除混合运算:有理数的乘除是同级运算,应按从________到________的顺序进行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=x+4的图象经过点(m,6),则m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a3(3an-2am+4ak)与3a6-2a9+4a4的值永远相等,则m、n、k分别为( )
A. 6、3、1 B. 3、6、1 C. 2、1、3 D. 2、3、1
相关试题

