【题目】如图,某校园的学子餐厅把![]() 密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络.
密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络.
(1)如果![]() 是2,那么他输入的密码是___________.
是2,那么他输入的密码是___________.
(2)若他输入的密码是4235![]() ,最后两位被隐藏了,那么被隐藏的两位数是_____.
,最后两位被隐藏了,那么被隐藏的两位数是_____.

参考答案:
【答案】![]() 77
77
【解析】
(1)根据前三个等式找出运算规律即可得;
(2)设等式左边三个数分别为![]() ,根据前面四位数字列出等式,从而可求出答案.
,根据前面四位数字列出等式,从而可求出答案.
设等式左边三个数分别为![]() ,则左边等式为
,则左边等式为![]()
由前三个已知等式可知,右边六位数可分成三部分:①最前两位数字等于![]() ;②中间两位数字等于
;②中间两位数字等于![]() ;③最后两位数字等于
;③最后两位数字等于![]()
(1)当![]() 时
时
则最前两位数字等于![]() ;中间两位数字等于
;中间两位数字等于![]() ;最后两位数字等于
;最后两位数字等于![]()
因此,这个六位数为![]()
(2)由题意得:![]()
则![]()
即被隐藏的两位数是77
故答案为:![]() ;77.
;77.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备了50个签,其中甲类、乙类、丙类按名额设置、25个空签,采取抽签的方式来确定名额分配,请解决下列问题
(1)该班小明同学恰好抽到丙类名额的概率是多少?
(2)该班小丽同学能有幸去参加游学活动的概率是多少?
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到20%,则还要争取甲类名额多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】声音在空气中传播的速度简称音速,实验测得音速与气温的一些数据如下表

(1)此表反映的是变量 随 变化的情况.
(2)请直接写出y与x的关系式为 .
(3)当气温为22℃时,某人看到烟花燃放5秒后才听到声响,求此人与烟花燃放所在地的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE,CF交于点D,过A点作AM⊥BD于M.
(1)探究∠BDC和∠CAB的数量关系并说明理由;
(2)求证:BM=DM+DC;
(3)如图2,将射线BE,CF分别绕点B和点C顺时针旋转至如图位置,若∠ABE=∠ACF仍然成立,射线BE交射线CF的反向延长线于点D,过A点作AM⊥BD于M.请问(2)中的结论是否还成立?如果成立,请证明.如果不成立,线段BM,DM,DC又有怎样的数量关系?并证明你的结论.
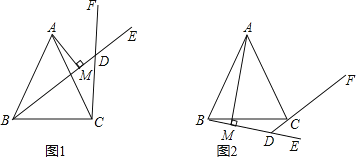
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“♀”,观察下列运算:
(+5)♀(+14)=+19,
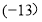 ♀
♀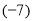 =+20,
=+20,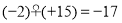 ,
,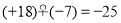 ,
,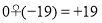 ,
,(+13)♀0=+13.
(1)请你认真思考上述运算,归纳运算“♀”的法则.
两数进行运算“♀”时,同号______,异号_________,特别地,0和任何数进行运算“♀”,或任何数和0进行运算“♀”,结果都为_______.
(2)计算:
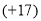 ♀[0♀
♀[0♀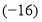 ].
]. -
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在纸面上有一数轴如图所示.

尝试:折叠纸面,使表示1的点与表示
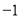 的点重合,则表示
的点重合,则表示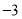 的点与表示_________的点重合.
的点与表示_________的点重合.发现:折叠纸面,使表示
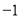 的点与表示3的点重合,则表示5的点与表示____________的点重合.
的点与表示3的点重合,则表示5的点与表示____________的点重合.应用:若数轴上
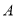 、
、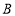 两点之间的距离为11(
两点之间的距离为11(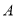 在
在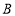 左侧),且经过折叠后,表示
左侧),且经过折叠后,表示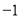 的点与表示3的点重合,点
的点与表示3的点重合,点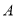 与点
与点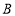 重合,分别求
重合,分别求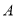 、
、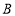 两点表示的数.
两点表示的数.
相关试题

