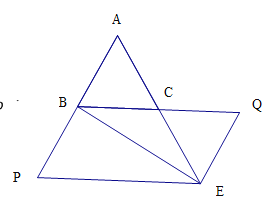
【题目】如图,△![]() 是等边三角形,
是等边三角形, ![]() =2
=2![]() .点
.点![]() 从点
从点![]() 出发沿沿射线
出发沿沿射线![]() 以1
以1 ![]() 的速度运动,过点
的速度运动,过点![]() 作
作![]() ∥
∥![]() 交射线
交射线![]() 于点
于点![]() ,同时点
,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 的延长线以1
的延长线以1 ![]() 的速度运动,连结
的速度运动,连结![]() 、
、![]() .设点
.设点![]() 的运动时间我
的运动时间我![]() (
(![]() ).
).
(1)求证:△![]() 是等边三角形;
是等边三角形;
(2)直接写出![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点![]() 在边
在边![]() 上,且不与点
上,且不与点![]() 、
、![]() 重合时,求证:△
重合时,求证:△![]() ≌△
≌△![]() .
.
(4)在不添加字母和连结其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.

参考答案:
【答案】(1)证明见解析;
(2)![]() 或
或![]() ;
;
(3)证明见解析;
(4)当t=1时,图中有5个等腰三角形,当t=4时,图中有4个等腰三角形.
【解析】【试题分析】
(1)△ABC是等边三角形,根据等边三角形的定义得:∠A=∠ABC=60°.
由于![]() ,根据两直线平行,同位角相等得:∠APE=∠ABC=60°.
,根据两直线平行,同位角相等得:∠APE=∠ABC=60°.
因为∠A=∠APE=60°.根据等边三角形的判定得:△APE是等边三角形.
(2)由题意得:AE=AP=t,当t<2时,CE= ![]() ;当t>2时,CE=
;当t>2时,CE= ![]() .
. ![]() 或
或![]() .
.
(3)根据△ABC是等边三角形,得到,AB=AC,∠ACB=60°.因为△APE是等边三角形,
得AP=PE=AE,∠APE=60°.则AB-AP=AC-AE,∠BPE=∠ECQ=120°.根据等量相减仍是等量得:BP=EC.由于AP=CQ=t,所以PE=CQ.根据SAS得,△BPE≌ECQ.
(4)当t=1时,图中有5个等腰三角形. ![]()
当t=4时,如图,图中有4个等腰三角形. ![]()
【试题解析】
(1)∵△ABC是等边三角形,
∴∠A=∠ABC=60°.
∵![]() ,
,
∴∠APE=∠ABC=60°.
∴∠A=∠APE=60°.
∴△APE是等边三角形.
(2)当t<2时,CE= ![]() ;当t>2时,CE=
;当t>2时,CE= ![]() .
.
(3)∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∵△APE是等边三角形,
∴AP=PE=AE,∠APE=60°.
∴AB-AP=AC-AE,∠BPE=∠ECQ=120°.
∴BP=EC.
∵AP=CQ=t,
∴PE=CQ.
∴△BPE≌ECQ.
(4)当t=1时,图中有5个等腰三角形.
当t=4时,如图,图中有4个等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a1 , a2 , a3 , a4 , …满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2016的值为( )
A.﹣1007
B.﹣1008
C.﹣1009
D.﹣1010 -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2向左平移2个单位,再向下平移5个单位,则平移后所得新抛物线的表达式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以A,B,C,D为顶点组成平行四边形,A(1,0),B(3,0),C(4,3),求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】题目:如图①,在四边形
 中,
中,  =
= ,∠
,∠ =∠
=∠ ,那么
,那么 =
= 吗?请说明理由.
吗?请说明理由.小明的作法如下:
如图②,连结
 .
.∵
 =
= ,∠
,∠ =∠
=∠ ,
, 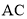 =
= .
.∴△
 ≌△
≌△ .
.所以
 =
= .
.(1)小明的作法错误的原因是 .
(2)请正确解答这道题目.

-
科目: 来源: 题型:
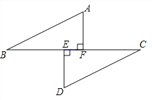
查看答案和解析>>【题目】如图,已知点
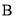 、
、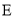 、
、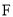 、
、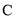 依次在同一条直线上,
依次在同一条直线上, 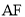 ⊥
⊥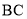 于点
于点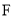 ,
, 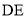 ⊥
⊥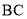 于点
于点 ,且
,且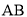 =
=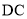 ,
, 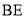 =
=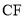 .
.(1)求证:
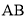 ∥
∥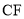 ;
;(2)连结
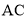 、
、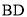 ,求证:
,求证: 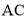 =
=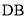 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=37°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)

相关试题

