【题目】已知,矩形OABC在平面直角坐标系内的位置如图所示,点O为坐标原点,点A的坐标示为(10,0),点B的坐标为(10,8) .
(1)直接写出点C的坐标为:C( ____ ,_____);
(2)已知直线AC与双曲线y=![]() (m≠0)在第一象限内有一点交点Q为(5,n),
(m≠0)在第一象限内有一点交点Q为(5,n),
①求m及n的值;
②若动点P从A点出发,沿折线AO→OC→CB的路径以每秒2个单位长度的速度运动,到达B处停止,△APQ的面积为S,当t取何值时,S=10.

参考答案:
【答案】(1)B(0,8) (2)![]() t=2.5s,7s,11.5s
t=2.5s,7s,11.5s
【解析】
(1)根据矩形的对边相等的性质直接写出点C的坐标;
(2)①设直线AC的解析式为y=kx+b(k≠0).将A(10,0)、C(0,8)两点代入其中,即利用待定系数法求一次函数解析式;然后利用一次函数图象上点的坐标特征,将点Q代入函数关系式求得n值;最后将Q点代入双曲线的解析式,求得m值;
②分类讨论:分当0≤t≤5时,当5<t≤9时,当9<t≤14时三种情况讨论求解.
(1)B(10,8) ,

(2)① 设直线AC 函数表达式为![]() (
(![]() ),
),
∵ 图像经过A(10,0).C(0,8),
∴![]() , 解得
, 解得 ,
,
∴![]() ,
,
当![]() 时,
时,![]() .
.
∵ Q(5,4)在![]() 上
上
∴![]() ,
,
∴![]() ;
;
②㈠当0<t≤5时,
AP=2t ,
∴![]() ,
,
∴4t=10,
∴t=2.5 ,
㈡当5<t≤9时,
OP=2t-10,CP=18-2t,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴t=7 ;
㈢当9<t≤14时,
OP=2t-18,BP=28-2t,
∴![]() ,
,
∴![]() ,
,
∴t=11.5 ,
综上所述:当t=2.5s,7s,11.5s时,△APQ的面积是10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰△ABC中,当顶角A的大小确定时,它的对边BC与邻边(腰AB或AC)的比值确定,记为f(A),易得f(60°)=1.若α是等腰三角形的顶角,则f(α)的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2017+3(tan60°)﹣1﹣|1﹣
 |+(3.14﹣π)0 .
|+(3.14﹣π)0 . -
科目: 来源: 题型:
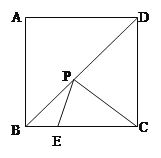
查看答案和解析>>【题目】如图,正方形ABCD的边长为
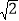 ,点P为对角线BD上一动点,点E在射线BC上,
,点P为对角线BD上一动点,点E在射线BC上,(1)填空:BD=______;
(2)若BE=t,连结PE、PC,求PE+PC的最小值(用含t的代数式表示);
(3)若点E是直线AP与射线BC的交点,当△PCE为等腰三角形时,求∠PEC的度数.
-
科目: 来源: 题型:
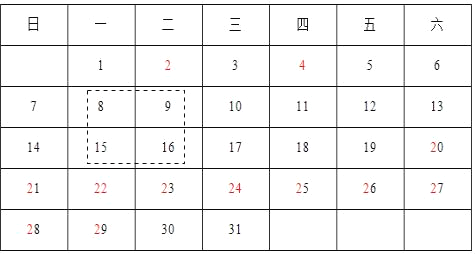
查看答案和解析>>【题目】如图所示为2013年7月份的日历示意图.
(1)请你计算虚线方框圈出的2×2个数(2行2列的4个数)的和;
(2)若方框圈出的2×2个数从左下角到右上角的2个数之和为46,则这4个数的最后一天是7月 日.(直接填空)
(3)若方框圈出的2×2个数的和最大,请你用方框将这4个数圈出来,并计算这4个数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,绵阳市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
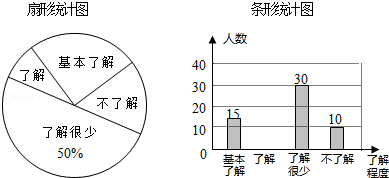
(1)接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;
(2)请补全条形统计图;
(3)若该中学共有学生3000人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=x+m的图象与反比例函数y2=
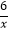 的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2 .
的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2 .
(1)求一次函数的函数表达式;
(2)已知反比例函数在第一象限的图象上有一点C到x轴的距离为2,求△ABC的面积.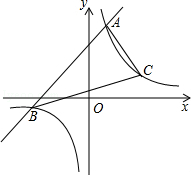
相关试题

