【题目】如图,在Rt△ABC中,∠BAC=90°,现在有一足够大的直角三角板,它的直角顶点D是BC上一点,另两条直角边分别交AB、AC于点E、F.
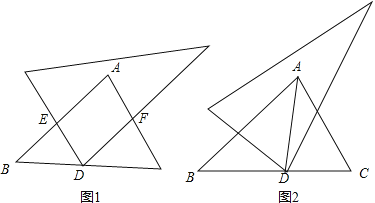
(1)如图1,若DE⊥AB,DF⊥AC,求证:四边形AEDF是矩形;
(2)在(1)条件下,若点D在∠BAC的 角平分线上,试判断此时四边形AEDF的形状,并说明理由;
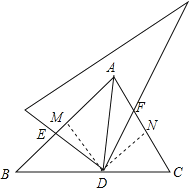
(3)若点D在∠BAC的角平分线上,将直角三角板绕点D旋转一定的角度,使得直角三角板的两条边与两条直角边分别交于点E、F(如图2),试证明AE+AF=![]() AD.
AD.
参考答案:
【答案】见解析
【解析】解:(1)∵DE⊥AB,BF⊥AC,
∴∠AED=∠AFD=90°,
∵∠BAC=90°,
∴四边形AEDF是矩形;
(2)四边形AEDF是正方形,
理由:∵点D在∠BAC的 角平分线上,DE⊥AB,BF⊥AC,
∴DE=DF,
∴矩形AEDF是正方形;
(3)作DM⊥AB于M,DN⊥AC于N,
∴∠AED=∠AFD=∠BAC=90°,
∵点D在∠BAC的 角平分线上,
∴DM=DN,
∴四边形AMDN是正方形,
∴AM=DM=DN=AN,∠MDN=∠AMD=90°,
∴∠MDF+∠NDF=90°,
∵∠EDF=90°,
∴∠MDF+∠EDM=90°,
∴∠NDF=∠EDM,
在△EMD与△END中, ,
,
∴△EMD≌△END,
∴EM=FN,
∵∠AMD=90°,
∴AM2+DM2=AD2,
∴AD=![]() AM,
AM,
∵AM=![]() (AM+AN)=
(AM+AN)=![]() (AE+AF),
(AE+AF),
∴AD=![]() ×
×![]() (AE+AF),
(AE+AF),
∴AE+AF=![]() AD.
AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,若CD=5,则四边形ABCD的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】码头工人往一艘轮船上装载货物,装完货物所需时间y(h)与装载速度x(t/h)之间的函数关系如图.

(1)这批货物的质量是多少?写出y与x之间的函数表达式;
(2)中午12:00轮船到达目的地后,接到气象部门预报,晚上8:00港口将受到台风影响必须停止卸货,为确保这批货物安全卸货,如果以8t/h的速度卸货,那么在台风到来之前能否卸完这批货?如果要在台风到来前卸完这批货,那么每小时至少要卸多少吨的货?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题,
例题:若
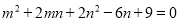 ,求
,求 和
和 的值.
的值.解:∵

∴

∴
 ∴
∴
∴

问题(1)若△ABC的三边长
 都是正整数,且满足
都是正整数,且满足 ,请问△ABC是什么形状?说明理由.
,请问△ABC是什么形状?说明理由.(2)若
 ,求
,求 的值.
的值.(3)已知
 ,则
,则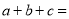 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】命题“等腰三角形两底角相等”的逆命题是 , 这个逆命题是命题;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句是命题的是( )
A.作直线AB的垂线
B.在线段AB上取点C
C.同旁内角互补
D.垂线段最短吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】元旦节班上数学兴趣小组的同学,互赠新年贺卡,每两个同学都相互赠送一张,小明统计出全组共互送了90张贺年卡,那么数学兴趣小组的人数是多少设数学兴趣小组人数为x人,则可列方程为( )
A.x(x﹣1)=90
B.x(x﹣1)=2×90
C.x(x﹣1)=90÷2
D.x(x+1)=90
相关试题

