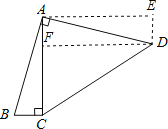
【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,若CD=5,则四边形ABCD的面积为 .

参考答案:
【答案】10
【解析】解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,
∵∠BAD=∠CAE=90°,
即∠BAC+∠CAD=∠CAD+∠DAE,
∴∠BAC=∠DAE,
在△ABC和△ADE中
∵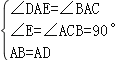 ,
,
∴△ABC≌△ADE(AAS),
∴BC=DE,AC=AE,
设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,
在Rt△CDF中,由勾股定理得:CF2+DF2=CD2,
即(3a)2+(4a)2=52,
解得:a=1,
∴S四边形ABCD=S梯形ACDE=![]() ×(DE+AC)×DF
×(DE+AC)×DF
=![]() ×(a+4a)×4a
×(a+4a)×4a
=10a2
=10.
故答案为:10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=2是x方程mx-4=3m解,则m=__________ ,
-
科目: 来源: 题型:
查看答案和解析>>【题目】要证明命题“若a>b,则a2>b2”是假命题,下列a,b的值不能作为反例的是( )
A.a=1,b=﹣2
B.a=0,b=﹣1
C.a=﹣1,b=﹣2
D.a=2,b=﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OBCD的顶点B、D坐标分别是(8,0)、(0,4),反比例函数y=
 (x>0)的图象过对角线的交点A并且与DC、BC分别交于E、F两点,连结OE、OF、EF,则△OEF的面积为______.
(x>0)的图象过对角线的交点A并且与DC、BC分别交于E、F两点,连结OE、OF、EF,则△OEF的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】码头工人往一艘轮船上装载货物,装完货物所需时间y(h)与装载速度x(t/h)之间的函数关系如图.

(1)这批货物的质量是多少?写出y与x之间的函数表达式;
(2)中午12:00轮船到达目的地后,接到气象部门预报,晚上8:00港口将受到台风影响必须停止卸货,为确保这批货物安全卸货,如果以8t/h的速度卸货,那么在台风到来之前能否卸完这批货?如果要在台风到来前卸完这批货,那么每小时至少要卸多少吨的货?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题,
例题:若
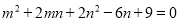 ,求
,求 和
和 的值.
的值.解:∵

∴

∴
 ∴
∴
∴

问题(1)若△ABC的三边长
 都是正整数,且满足
都是正整数,且满足 ,请问△ABC是什么形状?说明理由.
,请问△ABC是什么形状?说明理由.(2)若
 ,求
,求 的值.
的值.(3)已知
 ,则
,则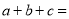 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,现在有一足够大的直角三角板,它的直角顶点D是BC上一点,另两条直角边分别交AB、AC于点E、F.
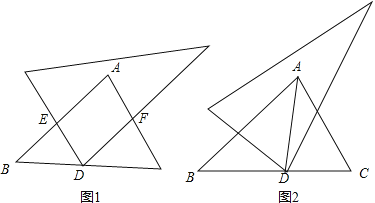
(1)如图1,若DE⊥AB,DF⊥AC,求证:四边形AEDF是矩形;
(2)在(1)条件下,若点D在∠BAC的 角平分线上,试判断此时四边形AEDF的形状,并说明理由;
(3)若点D在∠BAC的角平分线上,将直角三角板绕点D旋转一定的角度,使得直角三角板的两条边与两条直角边分别交于点E、F(如图2),试证明AE+AF=
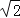 AD.
AD.
相关试题

