Question

【题目】如图，抛物线y=x2﹣3x+ 与x轴相交于A、B两点，与y轴相交于点C，点D是直线BC下方抛物线上一点，过点D作y轴的平行线，与直线BC相交于点E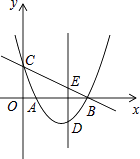

（1）求A、B的坐标；
（2）求直线BC的解析式；
（3）当线段DE的长度最大时，求点D的坐标．

Answer 1

【答案】
（1）解：当y=0时，x2﹣3x+ =0，解得x1= ，x2= ，

∴A（ ，0），B（ ，0）

（2）解：当x=0，则y=x2﹣3x+ = ，

∴C点坐标为（0， ），

设直线BC的解析式为y=kx+b，根据题意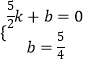得 ，解得 ，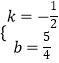

∴直线BC的解析式为：y=﹣ x+

（3）解：设点D的横坐标为m，则纵坐标为（m，m2﹣3m+ ），则E点的坐标为（m，﹣ m+ ），

DE=﹣ m+ ﹣（m2﹣3m+ ）=﹣m2+ m，

∵DE=﹣（m﹣ ）2+

∴m= 时，DE的长最大，

∴D点的坐标为（ ，﹣ ）

【解析】（1）通过解方程x2﹣3x+ =0可确定A点和B点坐标；（2）先求出C点坐标，然后利用待定系数法求直线BC的解析式；（3）设点D的横坐标为m，则纵坐标为（m，m2﹣3m+ ），则E点的坐标为（m，﹣ m+ ），则可利用m表示出DE，然后利用二次函数的性质求出m，从而可得到D点坐标．