【题目】如图,蚂蚁在5×5的方格(每个小方格的边长均为1 cm)上沿着网格线运动.它从A处出发去寻找B,C,D处的伙伴,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)A→D(________,________);D→B(________,________);C→B(________,________).
(2)若蚂蚁的行走路线为A→B→C→D,请计算蚂蚁走过的路程.
(3)若蚂蚁从A处出发去寻找伙伴,它的行走路线依次为(+1,+2),(+3,-1),(-2,+2),请在图中标出这只蚂蚁伙伴的位置E.
(4)在(3)中,若蚂蚁每走1 cm需要消耗1.5焦耳的能量,则蚂蚁在寻找伙伴E的过程中总共需要消耗多少焦耳的能量?

参考答案:
【答案】(1)(+4,+2);(-3,+2);(-2,0).
(2) 10(cm).
(3)详见解析.
(4) 16.5(焦耳).
【解析】
(1)理解题意辨明方向,确定第一个数和第二个数各自代表的方向,结合各点的位置解答题目;(2)明确A→B,B→C,C→D的行走方式,将各段走的路相加即为蚂蚁走过的路程;(3)根据所给的行走路线,确定蚂蚁如何从A开始行走,最后停留的位置即为这只蚂蚁的伙伴的位置E;(4)根据(2)中的方法求出行走的路程,然后乘以1.5焦耳得到一共需要消耗多少焦耳的能量.
(1)A→D(+4,+2);D→B(-3,+2);C→B(-2,0).
(2)蚂蚁走过的路程为1+4+2+0+1+2=10(cm).
(3)如图所示.

(4)蚂蚁走过的路程为1+2+3+1+2+2=11(cm),所以蚂蚁在寻找伙伴E的过程中总共需要消耗的能量为11×1.5=16.5(焦耳).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知有两人分别骑自行车和摩托车沿着相同的路线从甲地到乙地,如图反映的是这两个人在行驶过程中时间和路程的关系,请根据图象回答下列问题:
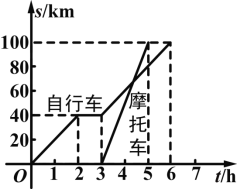
(1)甲地与乙地相距多少千米?两人分别用了几个小时才到达乙地?谁先到达乙地?先到者早到多长时间?
(2)分别描述在这个过程中自行车和摩托车的行驶状态;
(3)求摩托车行驶的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,AB=AD,∠BAD=60°,∠ABC=∠ADC=90°,点E、F分別在线段BC、CD上,∠EAF=30°,连接EF.

(1)如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′(A′B′与AD重合),那么
①∠E′AF度数②线段BE、EF、FD之间的数量关系
(2)如图3,当点E、F分别在线段BC、CD的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 (k为常数).
(k为常数).(1)k为何值时,该函数是正比例函数;
(2)k为何值时,正比例函数过第一、三象限,写出正比例函数解析式;
(3)k为何值时,正比例函数y随x的增大而减小,写出正比例函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣3x+
 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E 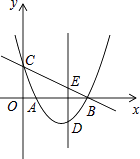
(1)求A、B的坐标;
(2)求直线BC的解析式;
(3)当线段DE的长度最大时,求点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B,C,D分别表示-3,-1
 ,0,4.请解答下列问题:
,0,4.请解答下列问题:(1)在数轴上描出A,B,C,D四个点;
(2)现在把数轴的原点取在点B处,其余均不变,那么点A,B,C,D分别表示什么数?
相关试题

