【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).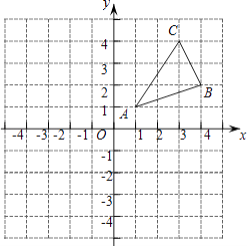
①画出△ABC关于y轴的对称图形△A1B1C1 , 并写出B1点的坐标;
②画出△ABC绕原点O旋转180°后得到的图形△A2B2C2 , 并写出B2点的坐标;
③在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.
参考答案:
【答案】解:△A1B1C1、△A2B2C2、△PAB如图所示,B1(﹣4,2);B2(﹣4,﹣2);P(2,0).
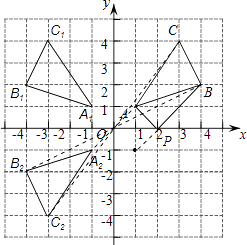
【解析】①分别作出点A、B、C关于y轴的对称点A1、B1、C1,然后顺次连接,并写出B1点的坐标。
(2)画出△ABC绕原点O旋转180°后得到的图形△A2B2C2,就是作出△ABC关于原点对称的△A2B2C2,并写出B2点的坐标。
(3)找出点A关于x轴的对称点A′,连接A′B与x轴相交于一点,根据轴对称确定最短路线问题,交点即为所求的点P的位置,然后连接AP、BP,根据图像写出点P的坐标即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣4≥0的解集是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两边长分别为3和7,第三边长为整数,则第三边长度的最小值是( )
A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)求点A坐标及抛物线的解析式.
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将多项式﹣5a2bc+3ab2﹣abc各项提公因式后,另一个因式是( )
A.5ac﹣3ab+c
B.5bc﹣3b+c
C.﹣5ac+3b+c
D.﹣5bc+3b+c -
科目: 来源: 题型:
查看答案和解析>>【题目】图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时)。
(1)用有序实数对表示图中各点。
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?

-
科目: 来源: 题型:
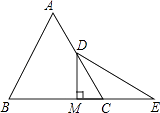
查看答案和解析>>【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点.
相关试题

