【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点.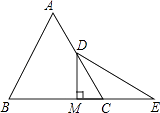
参考答案:
【答案】证明:连接BD,
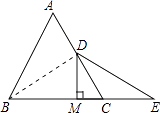
∵在等边△ABC,且D是AC的中点,
∴∠DBC= ![]() ∠ABC=
∠ABC= ![]() ×60°=30°,∠ACB=60°,
×60°=30°,∠ACB=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠CDE+∠E,
∴∠E=30°,
∴∠DBC=∠E=30°,
∴BD=ED,△BDE为等腰三角形,
又∵DM⊥BC,
∴M是BE的中点.
【解析】要证M是BE的中点,根据题意可知,证明△BDE△为等腰三角形,利用等腰三角形三线合一的性质即可得证。
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
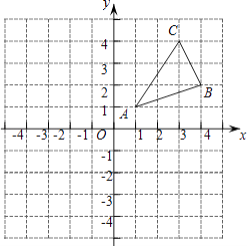
①画出△ABC关于y轴的对称图形△A1B1C1 , 并写出B1点的坐标;
②画出△ABC绕原点O旋转180°后得到的图形△A2B2C2 , 并写出B2点的坐标;
③在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】将多项式﹣5a2bc+3ab2﹣abc各项提公因式后,另一个因式是( )
A.5ac﹣3ab+c
B.5bc﹣3b+c
C.﹣5ac+3b+c
D.﹣5bc+3b+c -
科目: 来源: 题型:
查看答案和解析>>【题目】图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时)。
(1)用有序实数对表示图中各点。
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?

-
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣2)2013+(﹣2)2014的值为( )
A.2
B.﹣2
C.﹣22013
D.22013 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:6÷(﹣3)+|﹣1|﹣20150 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
∵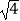 <
< 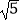 <
<  ,即2<
,即2< 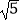 <3.
<3.
∴1<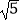 ﹣1<2
﹣1<2
∴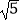 ﹣1的整数部分为1.
﹣1的整数部分为1.
∴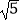 ﹣1的小数部分为
﹣1的小数部分为 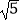 ﹣2.
﹣2.
解决问题:
已知a是 ﹣3的整数部分,b是
﹣3的整数部分,b是  ﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
相关试题

