【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)求点A坐标及抛物线的解析式.
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
参考答案:
【答案】(1)y=﹣x2+2x+3 (2)当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形 (3)t=2
时,△PCQ为直角三角形 (3)t=2
【解析】(1)由抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,可求得点A的坐标,然后设抛物线的解析式为y=a(x﹣1)2+4,将点C代入即可求得答案;
(2)分别从∠QPC=90°与∠PQC=90°,利用cos∠QPC求解即可求得答案;
(3)首先设直线AC的解析式为y=kx+b,利用待定系数法即可求得直线AC的解析式,然后求得点Q的坐标,继而求得S△ACQ=S△AFQ+S△CPQ=![]() FQAG+
FQAG+![]() FQDG=
FQDG=![]() FQ(AG+DG)=
FQ(AG+DG)=![]() (t﹣2)2+1,则可求得答案.
(t﹣2)2+1,则可求得答案.
解:(1)∵抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,
∴点A坐标为(1,4),
设抛物线的解析式为y=a(x﹣1)2+4,
把C(3,0)代入抛物线的解析式,可得a(3﹣1)2+4=0,
解得a=﹣1.
∴抛物线的解析式为:y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(2)依题意有:OC=3,OE=4,
∴CE=![]() =5,
=5,
当∠QPC=90°时,
∵cos∠QPC=![]() ,
,
∴![]() ,
,
解得t=![]() ;
;
当∠PQC=90°时,
∵cos∠QCP=![]() ,
,
∴![]() ,
,
解得t=![]() .
.
∴当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形;
时,△PCQ为直角三角形;
(3)∵A(1,4),C(3,0),
设直线AC的解析式为y=kx+b,则![]() ,解得:
,解得: ![]() .
.
故直线AC的解析式为y=﹣2x+6.
∵P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得x=1+![]() ,
,
∴Q点的横坐标为1+![]() ,
,
将x=1+![]() 代入y=﹣(x﹣1)2+4中,得y=4﹣
代入y=﹣(x﹣1)2+4中,得y=4﹣![]() .
.
∴Q点的纵坐标为4﹣![]() ,
,
∴QF=(4﹣![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣![]() ,
,
∴S△ACQ=S△AFQ+S△CPQ=![]() FQAG+
FQAG+![]() FQDG=
FQDG=![]() FQ(AG+DG)=
FQ(AG+DG)=![]() FQAD=
FQAD=![]() ×2(t﹣
×2(t﹣![]() )=﹣
)=﹣![]() (t﹣2)2+1,
(t﹣2)2+1,
∴当t=2时,△ACQ的面积最大,最大值是1.
“点睛”考查了二次函数综合题,涉及的知识点有:抛物线的对称轴,矩形的性质,待定系数法求抛物线的解析式,待定系数法求直线的解析式,勾股定理,三角形面积,二次函数的最值,以及分类思想的运用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把b2(x﹣2)+b(2﹣x)分解因式的结果为( )
A.b(x﹣2)(b+1)
B.(x﹣2)(b2+b)
C.b(x﹣2)(b﹣1)
D.(x﹣2)(b2﹣b) -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣4≥0的解集是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两边长分别为3和7,第三边长为整数,则第三边长度的最小值是( )
A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
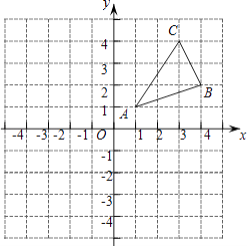
①画出△ABC关于y轴的对称图形△A1B1C1 , 并写出B1点的坐标;
②画出△ABC绕原点O旋转180°后得到的图形△A2B2C2 , 并写出B2点的坐标;
③在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】将多项式﹣5a2bc+3ab2﹣abc各项提公因式后,另一个因式是( )
A.5ac﹣3ab+c
B.5bc﹣3b+c
C.﹣5ac+3b+c
D.﹣5bc+3b+c -
科目: 来源: 题型:
查看答案和解析>>【题目】图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时)。
(1)用有序实数对表示图中各点。
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?

相关试题

