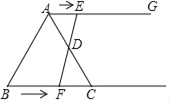
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,试判定四边形AFCE的形状并说明理由;
(2)当t为多少时,四边形ACFE是菱形.
参考答案:
【答案】(1)四边形AFCE是平行四边形.理由见解析;(2)t=6.
【解析】
(1)证△ADE≌△CDF(AAS),得DE=DF,从对角线角度证四边形AFCE是平行四边形;(2)根据菱形性质求解.
(1)解:四边形AFCE是平行四边形.
理由:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
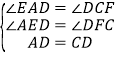 ,
,
∴△ADE≌△CDF(AAS),
∴DE=DF
∴四边形AFCE是平行四边形;
(2)解:若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s).
-
科目: 来源: 题型:
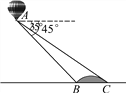
查看答案和解析>>【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈
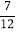 ,cos35°≈
,cos35°≈ ,tan35°≈
,tan35°≈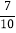 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:
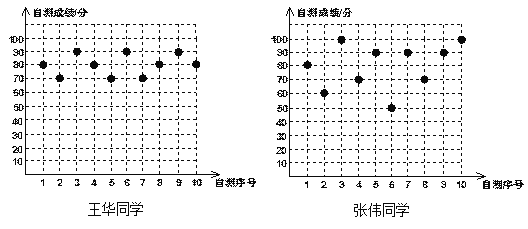
(1)根据上图中提供的数据列出如下统计表:
平均成绩(分)
中位数(分)
众数(分)
方差(S2)
王华
80
b
80
d
张伟
a
85
c
260
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在以点O为原点的数轴上,点A表示的数是3,点B在原点的左侧,且AB=6AO(我们把数轴上两点之间的距离用表示两点的大写字母一起标记,比如,点A与点B之间的距离记作AB).
(1)B点表示的数是_______.
(2)若动点P从O点出发,以每秒2个单位长度的速度匀速向左运动,问经过几秒钟后PA=3PB?并求出此时P点在数轴上对应的数.
(3)若动点M.P.N分别同时从A、O、B出发,匀速向右运动,其速度分别为1个单位长度/秒.2个单位长度/秒.4个单位长度/秒,设运动时间为t秒,请直接写出PM.PN.MN中任意两个相等时的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度
2013
2014
2015
2016
投入技改资金
 (万元)
(万元)2.5
3
4
4.5
产品成本
 (万元/件)
(万元/件)7.2
6
4.5
4
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:
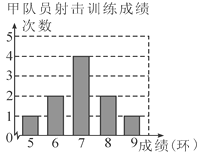

根据以上信息,整理分析数据如下:
平均成绩(环)
中位数(环)
众数(环)
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】刚刚升入初一,学习成绩优异但体育一般的王晴同学未雨绸缪,已经为将来的体育中考做起了准备.上周末她在家练习1分钟跳绳,以每分钟150下为基准,超过或不足的部分分别用正负数来表示,8次成绩(单位:下)分别是-10,-8,-5,-2,+2,+8,+3,-4.
(1)成绩最好的一次比最差的一次多跳多少下?
(2)求王晴这8次跳绳的平均成绩.
相关试题

