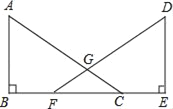
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.
求证:GF=GC.
参考答案:
【答案】证明见解析
【解析】
由AB⊥BE和DE⊥BE可得∠B=∠E=90°,由此可得△ABC和△DEF是直角三角形;又由BF=CE可得CB=EF,再加条件AC=DF,可以用HL定理证明Rt△ABC≌Rt△DEF,由此可以得到∠ACB=∠DFE,利用等角对等边可证出GF=GC.
证明:∵AB⊥BE
∴∠B=90°
∵DE⊥BE
∴∠E=90°
∵BF=CE
∴BF+CF=CE+CF
即:CB=EF
在Rt△ABC和Rt△DEF中![]() ,
,
∴Rt△ABC≌Rt△DEF(HL)
∴∠ACB=∠DFE
∴GF=CG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
像
 、
、 、
、 ……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如
……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如 与
与 ,
, 与
与 ,
, 与
与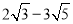 等都是互为有理化因式.
等都是互为有理化因式.在进行二次根式计算时,利用有理化因式,可以化去分母中的根号。
例如:
 ;
;
解答下列问题:
(1)
 与 互为有理化因式,将
与 互为有理化因式,将 分母有理化得
分母有理化得 (2)计算:

(3)观察下面的变形规律并解决问题:
①
 ,
, ,
, ,
, ……若
……若 为正整数,请你猜想
为正整数,请你猜想
②计算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
(1) 求证:CP是⊙O的切线;
(2) 若PC=6,AB=4
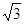 ,求图中阴影部分的面积.
,求图中阴影部分的面积.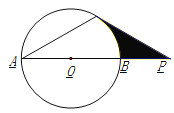
-
科目: 来源: 题型:
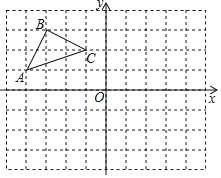
查看答案和解析>>【题目】按要求完成作图:
(1)作出△ABC关于x轴对称的图形;
(2)写出A、B、C的对应点A′、B′、C′的坐标;
(3)直接写出△ABC的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料解决问题:
材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).
(2)根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.
(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC、△BDE都是等腰直角三角形,∠ABC=∠DBE=90°,连接AE、CD交于点F,连接BF.求证:
(1)AE=CD;
(2)BF平分∠AFD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:


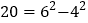
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中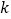 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
相关试题

