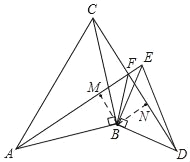
【题目】如图,△ABC、△BDE都是等腰直角三角形,∠ABC=∠DBE=90°,连接AE、CD交于点F,连接BF.求证:
(1)AE=CD;
(2)BF平分∠AFD.

参考答案:
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)由等腰直角三角形的性质可得AB=BC,BE=BD,∠ABC=∠DBE,由“SAS”可证△ABE≌△CBD,可得AE=CD;
(2)由全等三角形的性质可得S△ABE=S△CBD,可求BM=BN,由角平分线的性质可证BF平分∠AFD.
证明:(1)∵△ABC、△BDE都是等腰直角三角形
∴AB=BC,BE=BD,∠ABC=∠DBE
∴∠ABE=∠CBD,且AB=BC,BE=BD,
∴△ABE≌△CBD(SAS)
∴AE=CD;
(2)如图,过点B作BM⊥AE于M,BN⊥CD于N,
∵△ABE≌△CBD
∴S△ABE=S△CBD,
∴![]() AE×BM=
AE×BM=![]() CD×BN
CD×BN
∴BM=BN,且BM⊥AE,BN⊥CD
∴BF平分∠AFD.
-
科目: 来源: 题型:
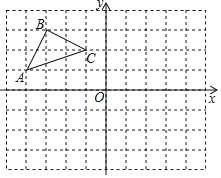
查看答案和解析>>【题目】按要求完成作图:
(1)作出△ABC关于x轴对称的图形;
(2)写出A、B、C的对应点A′、B′、C′的坐标;
(3)直接写出△ABC的面积 .
-
科目: 来源: 题型:
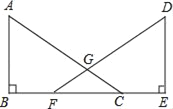
查看答案和解析>>【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.
求证:GF=GC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料解决问题:
材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).
(2)根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.
(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:


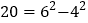
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中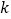 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人,在扇形统计图中“D”对应的圆心角的度数为 ;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).

-
科目: 来源: 题型:
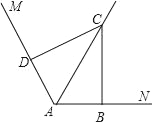
查看答案和解析>>【题目】(1)如图,已知∠MAN=120°,AC平分∠MAN,∠ABC=∠ADC=90°,则能得到如下两个结论:①DC=BC;②AD+AB=AC. 请你证明结论②.
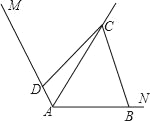
(2)如图,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
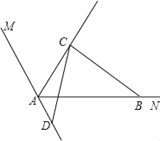
(3)如图3,如果D在AM的反向延长线上,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC=∠ADC,其他条件不变,(1)中的结论是否仍然成立?若成立,请直接回答;若不成立,你又能得出什么结论,直接写出你的结论.
相关试题

