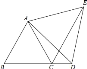
【题目】如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=6cm,求AD的长.

参考答案:
【答案】2
【解析】
根据等边对等角可得∠B=∠C,再利用三角形的内角和定理求出∠BAC=120°,然后求出∠CAD=30°,从而得到∠CAD=∠C,根据等角对等边可得AD=CD,再根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2AD,然后根据BC=BD+CD列出方程求解即可
∵AB=AC,
∴∠B=∠C=30°,
∴∠BAC=180°-2×30°=120°,
∵DA⊥BA,
∴∠BAD=90°,
∴∠CAD=120°-90°=30°,
∴∠CAD=∠C,
∴AD=CD,
在Rt△ABD中,
∵∠B=30°,∠BAD=90°,
∴BD=2AD,
∴BC=BD+CD=2AD+AD=3AD,
∵BC=6cm,
∴AD=2cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班参加一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分20分,题b、题c满分均为25分.竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,在这个班的平均成绩是__分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点分别为A(2,4),B(﹣2,2),C(3,1).
(1)作出△ABC关于x轴对称的图形△DEF,写出顶点D、E、F的坐标.
(2)如果点H(3m﹣1,n﹣6)与点H′(2n+7,3m﹣9)关于y轴对称,求m,n的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF.
(1)求△ABE的面积.
(2)求折痕EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边△ABC中,点D在BC边的延长线上,CE平分∠ACD,且CE=BD.判断△ADE的形状,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

相关试题

