【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( ) 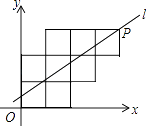
A.![]()
B.y= ![]() x+
x+ ![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C, ∵正方形的边长为1,
∴OB=3,
∵经过P点的一条直线l将这八个正方形分成面积相等的两部分,
∴三角形ABP面积是8÷2+1=5,
∴ ![]() BPAB=5,
BPAB=5,
∴AB=2.5,
∴OA=3﹣2.5=0.5,
由此可知直线l经过(0,0.5),(4,3)
设直线方程为y=kx+b,则 ![]() ,
,
解得 ![]() .
.
∴直线l解析式为y= ![]() x+
x+ ![]() .
.
故选B.
直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出点A的坐标,根据待定系数法即可得到该直线l的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.2a2+3a2=5a4
B.(a﹣b)2=a2﹣b2
C.(a3)3=a6
D.(﹣2a2)3=﹣8a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
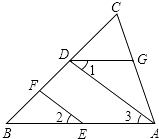
解:因为EF∥AD,
所以∠2=().
又因为∠1=∠2,
所以∠1=∠3().
所以AB∥().
所以∠BAC+=180°().
因为∠BAC=80°,
所以∠AGD= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为______cm2.
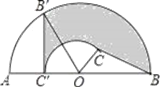
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
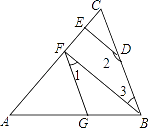
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数. -
科目: 来源: 题型:
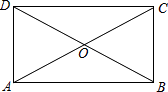
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,△AOD是正三角形,AD=4,则平行四边形ABCD的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果(3m+3n+2)(3m+3n-2)=77,那么m+n的值为________.
相关试题

