【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,△AOD是正三角形,AD=4,则平行四边形ABCD的面积为 . 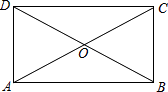
参考答案:
【答案】16 ![]()
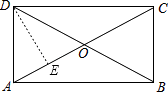
【解析】解:作DE⊥AC于E, ∴∠AED=90°.
∵△AOD是正三角形,
∴AD=DO=AO,AO=EO= ![]() AO,∠ADO=∠DAO=60°,
AO,∠ADO=∠DAO=60°,
∴∠ADE=30°.
∵AD=4,
∴AE=2.
在Rt△ADE中,由勾股定理,得
DE=2 ![]() ,
,
∴S△AOD= ![]() ×4×2
×4×2 ![]() =4
=4 ![]() .
.
∵四边形ABCD是平行四边,
∴S△AOD=S△DOC=S△BOC=S△AOB ,
∴平行四边形ABCD的面积=4×4 ![]() =16
=16 ![]() .
.
所以答案是:16 ![]() .
.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.
-
科目: 来源: 题型:
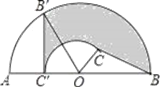
查看答案和解析>>【题目】如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为______cm2.
-
科目: 来源: 题型:
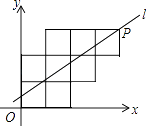
查看答案和解析>>【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A.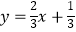
B.y= x+
x+ 
C.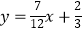
D.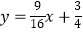
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
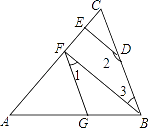
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果(3m+3n+2)(3m+3n-2)=77,那么m+n的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC与Rt△DEF的位置如图所示,其中AC=2
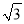 ,BC=6,DE=3
,BC=6,DE=3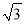 ,∠D=30°,其中,Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动,射线DE、DF与射线AB分别交于N、M两点,运动时间为t,当点E运动到与点B重合时停止运动.
,∠D=30°,其中,Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动,射线DE、DF与射线AB分别交于N、M两点,运动时间为t,当点E运动到与点B重合时停止运动.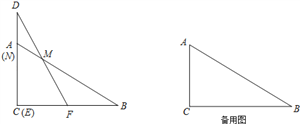
(1)当Rt△DEF在起始时,求∠AMF的度数;
(2)设BC的中点的为P,当△PBM为等腰三角形时,求t的值;
(3)若两个三角形重叠部分的面积为S,写出S与t的函数关系式和相应的自变量的取值范围.
-
科目: 来源: 题型:
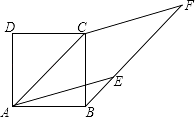
查看答案和解析>>【题目】如图,BF平行于正方形ABCD的对角线AC,点E在BF上,且AE=AC,CF∥AE,则∠BCF的度数为 .
相关试题

