【题目】已知正方形![]() ,
,![]() 为边
为边![]() 上一点
上一点![]() 不与
不与![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() .
.
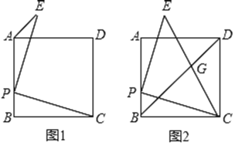
(1)如图1,求![]() 的度数;
的度数;
(2)如图2,连接![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(3)如图2,当![]() ,
,![]() ,则
,则![]() (直接写出结果)
(直接写出结果)
参考答案:
【答案】(1)∠EAD=45°;(2)证明见详解;(3)![]()
【解析】
(1)如图1中,作EH⊥BA于H.只要证明△HPE≌△CBP,推出BC=PH=AB,HE=PB,推出PB=AH=EH,推出∠HAE=45°,即可解决问题;
(2)作EK∥AB交BD于K.首先证明四边形ABKE是平行四边形,再证明△GEK≌△GCD,可得GD=GK,根据BD=![]() CD,即可解决问题;
CD,即可解决问题;
(3)利用(1)(2)中结论即可解决问题;
(1)如图1中,作EH⊥BA于H.
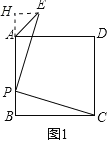
∵四边形ABCD是正方形,
∴∠B=∠BAD=∠HAD=90°,AB=BC,
∵EP⊥PC,
∴∠EPC=90°,
∴∠BPC+∠HPE=90°,∠BPC+∠BCP=90°,
∴∠HPE=∠BCP,
在△HPE和△CBP中,

∴△HPE≌△CBP,
∴BC=PH=AB,HE=PB,
∴PB=AH=EH,
∴∠HAE=45°,
∴∠EAD=45°.
(2)证明:作EK∥AB交BD于K.
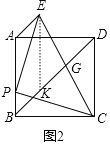
∵∠EAD=∠ADB=45°,
∴AE∥BK,
∵AB∥EK,
∴四边形ABKE是平行四边形,
∴EK=AB=CD,AE=BK,
∵AB∥CD,∴EK∥CD,
∴∠GEK=∠GCD,
∴△GEK≌△GCD,
∴GD=GK,
∵BD=![]() CD,BD=BK+DK=AE+2DG,
CD,BD=BK+DK=AE+2DG,
∴AE+2DG=![]() CD.
CD.
(3)由(1)可知AE=![]() ,由(2)可知
,由(2)可知![]() +2DG=
+2DG=![]() ,
,
∴DG=![]() ,
,
∵BD=![]() ,
,
∴BG=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
∵

∴

解答问题:
(1)在式
 中,第六项为 ,第n项为 ,上述求和的想法是通过逆用 法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以 从而达到求和的目的.
中,第六项为 ,第n项为 ,上述求和的想法是通过逆用 法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以 从而达到求和的目的.(2)解方程

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°∠DAB=45°.(1)求∠DAC的度数;(2)请说明:AB=CD.

-
科目: 来源: 题型:
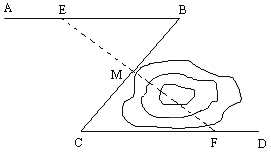
查看答案和解析>>【题目】在新修的花园小区中,有一条“Z”字形绿色长廊ABCD,如图,AB∥CD,在AB、BC、CD三段绿色长廊上各修建一凉亭E、M、F,且BE=CF,M是BC的中点,E、M、F在一条直线上.若在凉亭M与F之间有一池塘,在用皮尺不能直接测量的情况下,你能知道M与F之间的距离吗?试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作ECFG.
(1)如图1,证明ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,并求出∠BDG的度数:
(3)如图3,若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG= ,则梯形AECD的周长为( )
,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
相关试题

