【题目】阅读下列材料:
∵![]()
∴![]()
解答问题:
(1)在式![]() 中,第六项为 ,第n项为 ,上述求和的想法是通过逆用 法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以 从而达到求和的目的.
中,第六项为 ,第n项为 ,上述求和的想法是通过逆用 法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以 从而达到求和的目的.
(2)解方程![]()
参考答案:
【答案】(1)![]() ,
,![]() ,分式的加减法,相互抵消
,分式的加减法,相互抵消
(2)![]() 或
或![]()
【解析】
(1)观察式子可得,每一项的分母为相邻两个奇数的积,据此可得第六项,第![]() 项的表达式;而运算过程采用的是分式的加减法,达到相互抵消的目的
项的表达式;而运算过程采用的是分式的加减法,达到相互抵消的目的
(2)根据(1)的规律得出相互抵消后的结果,按照分式方程的解法运算即可
(1)第一空:根据以上分析可得,分母为相邻两个奇数的积;第一项分母为![]() ,第二项分母为
,第二项分母为![]() ,……,依此类推,得第六项分母为
,……,依此类推,得第六项分母为![]() ,故第六项为:
,故第六项为:![]()
第二空:又因为奇数的表示为![]() ,故相邻两个奇数的表示为:
,故相邻两个奇数的表示为:![]() ,
,![]() ,故第
,故第![]() 项的表示为:
项的表示为:![]()
第三空:运算过程是逆用分式的加减法,故填写:分式的加减法
第四空:运算过程是为了达到相互抵消的目的,故填写:相互抵消
(2)![]()
化简得:![]()
即:![]()
方程两边都乘![]() ,得
,得
![]()
解得:![]() 或
或![]()
检验:当![]() 时,
时, ![]()
![]()
当![]() ,
,![]()
![]()
故![]() 或
或![]() 是原分式方程的解
是原分式方程的解
故答案为:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-x+(k+13)和反比例函数
 的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.
的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.
(1)求反比例函数和一次函数的解析式;
(2)求点A与点B的坐标;
(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°∠DAB=45°.(1)求∠DAC的度数;(2)请说明:AB=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形
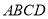 ,
,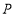 为边
为边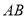 上一点
上一点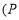 不与
不与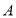 、
、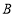 重合),过
重合),过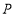 作
作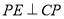 ,且
,且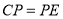 ,连接
,连接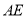 .
.(1)如图1,求
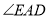 的度数;
的度数;(2)如图2,连接
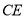 交
交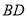 于
于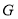 ,求证:
,求证: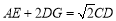 ;
;(3)如图2,当
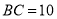 ,
,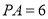 ,则
,则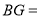 (直接写出结果)
(直接写出结果)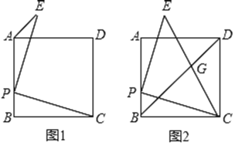
-
科目: 来源: 题型:
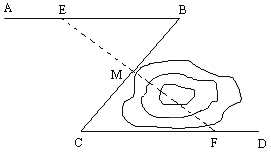
查看答案和解析>>【题目】在新修的花园小区中,有一条“Z”字形绿色长廊ABCD,如图,AB∥CD,在AB、BC、CD三段绿色长廊上各修建一凉亭E、M、F,且BE=CF,M是BC的中点,E、M、F在一条直线上.若在凉亭M与F之间有一池塘,在用皮尺不能直接测量的情况下,你能知道M与F之间的距离吗?试说明理由.
相关试题

