【题目】某商场准备进一批两种不同型号的衣服,已知购进![]() 种型号衣服9件,
种型号衣服9件,![]() 种型号衣服10件,则共需1810元;若购进
种型号衣服10件,则共需1810元;若购进![]() 种型号衣服12件,
种型号衣服12件,![]() 种型号衣服8件,共需1880元;已知销售一件
种型号衣服8件,共需1880元;已知销售一件![]() 型号衣服可获利18元,销售一件
型号衣服可获利18元,销售一件![]() 型号衣服可获利30元.要使在这次销售中获利不少于699元,且
型号衣服可获利30元.要使在这次销售中获利不少于699元,且![]() 型号衣服不多于28件.
型号衣服不多于28件.
(1)求![]() 型号衣服进价各是多少元?
型号衣服进价各是多少元?
(2)若已知购进![]() 型号衣服是
型号衣服是![]() 型号衣服的2倍还多4件,则商店在这次进货中可有几种方案?并简述购货方案.
型号衣服的2倍还多4件,则商店在这次进货中可有几种方案?并简述购货方案.
参考答案:
【答案】(1)![]() 型号衣服每件90元,
型号衣服每件90元,![]() 型号衣服每件100元;(2)有三种进货方案:①
型号衣服每件100元;(2)有三种进货方案:① ![]() 型号衣服购买10件,
型号衣服购买10件,![]() 型号衣服购进24件;②
型号衣服购进24件;②![]() 型号衣服购买11件,
型号衣服购买11件,![]() 型号衣服购进26件;③
型号衣服购进26件;③![]() 型号衣服购买12件,
型号衣服购买12件,![]() 型号衣服购进28件.
型号衣服购进28件.
【解析】
(1)等量关系为:A种型号衣服9件×进价+B种型号衣服10件×进价=1810,A种型号衣服12件×进价+B种型号衣服8件×进价=1880;
(2)关键描述语是:获利不少于699元,且A型号衣服不多于28件.关系式为:18×A型件数+30×B型件数≥699,A型号衣服件数≤28.
(1)设![]() 型号衣服每件
型号衣服每件![]() 元,
元,![]() 型号衣服每件
型号衣服每件![]() 元,
元,
则:![]() 解得
解得![]()
答:![]() 型号衣服每件90元,
型号衣服每件90元,![]() 型号衣服每件100元
型号衣服每件100元
(2)设![]() 型号衣服购进
型号衣服购进![]() 件,则
件,则![]() 型号衣服购进
型号衣服购进![]() 件,
件,
则: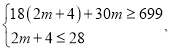 解得
解得![]()
![]() 为正整数,
为正整数,
![]() 、11、12,
、11、12,![]() 24、26、28.
24、26、28.
答:有三种进货方案:
①![]() 型号衣服购买10件,
型号衣服购买10件,![]() 型号衣服购进24件;
型号衣服购进24件;
②![]() 型号衣服购买11件,
型号衣服购买11件,![]() 型号衣服购进26件;
型号衣服购进26件;
③ ![]() 型号衣服购买12件,
型号衣服购买12件,![]() 型号衣服购进28件.
型号衣服购进28件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
(1)如图①,点M、N分别为四边形ABCD边AD、BC的中点,则四边形BNDM的面积与四边形ABCD的面积关系是 .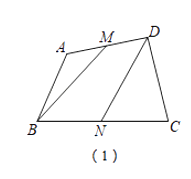
(2)如图②,在四边形ABCD中,点M、N分别为AD、BC的中点,MB交AN于点P,MC交DN于点Q,若S△四边形MPNQ=10,则S△ABP+S△DCQ的值为多少?
(3)问题解决
在矩形ABCD中,AD=2,DC=4,点M、N为AB上两点,且满足BN=2AM=2MN,连接MC、MD.若点P为CD上任意一点,连接AP、NP,使得AP与DM交于点E,NP与MC交于点F,则四边形MEPF的面积是否存最大值?若存在,请求出最大面积;若不存在,请说明理由.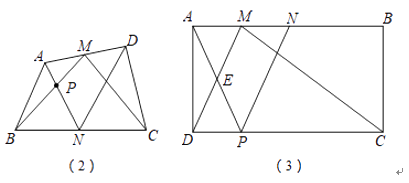
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,交AC于点E,连接CD,则CD=( )

A.3
B.4
C.4.8
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式:
第1个式子:
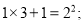
第2个式子:
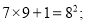
第3个式子:
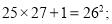
第4个式子:


(1)可猜想第7个等式为 .
(2)探索规律,若字母
 表示自然数,请写出第
表示自然数,请写出第 个等式 .
个等式 . (3)试证明你写出的等式的正确性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=6,将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF,延长DA交FG于点H,则GH的长为( )
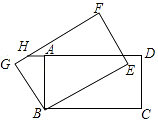
A.8﹣4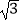
B.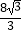 ﹣4
﹣4
C.3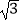 ﹣4
﹣4
D.6﹣3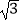
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型价格
A型
B型
进价(元/件)
60
100
标价(元/件)
100
160
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
相关试题

